26/01/2022 (2021-10-25)
Par Karen Brandin
Quel que soit le chemin qui nous aura finalement conduit un jour à nous présenter devant un parterre d’élèves avec l’envie, l’espoir, le devoir, la responsabilité toujours de transmettre de manière motivée et loyale un peu de mathématiques, nous avons tous à un moment emprunté de manière joyeuse souvent, douloureuse parfois, celui escarpé de l’algèbre. On a alors forcément croisé la route de la notion de groupe tout d’abord ; un enfant terrible, un peu insaisissable, à l’origine d’une théorie aussi difficile que riche, et qu’étudiante je trouvais redoutable parce « qu’instable ».
Dans un groupe, on se rassemble bien sûr par « caractères », par « classes d’équivalence », mais tout en gardant son identité et une certaine indépendance aussi. Il peut donc y avoir des tensions, car après tout, il n’y a qu’une loi interne pour régir l’ensemble.
Quand nous avons ensuite abordé la notion d’anneaux, je me souviens avoir été soulagée. On avait rigidifié le cadre ; c’était un peu comme si l’on avait ajouté un angle à une figure et avec lui, la possibilité nouvelle de se réfugier en cas de menace. Avec l’anneau, qu’il soit factoriel, principal ou noethérien, on devinait les prémisses d’une structure « idéale. »
Sont ensuite venus, dans cette maladroite esquisse d’une hiérarchie algébrique aussi partielle qu’imparfaite, les corps. De nombres ou de fonctions, on pouvait les étendre, les décomposer, mais dans tous les cas, on avait à faire à une structure stable, fiable, sur laquelle on pouvait s’appuyer ; une structure garante d’une certaine homogénéité.
Si j’évoque en préambule ces notions si peu présentes au lycée ou alors seulement en filigrane, c’est parce que l’on parle bel et bien du « Corps enseignant », du « Corps professoral » et que cela suggère peut-être qu’il est plus que temps de renouer avec la volonté, le courage, mais aussi une forme de solidarité intra et interdisciplinaire. Car en plus de masquer durablement les visages, les sourires et les expressions, la crise dite sanitaire, désormais suivie d’une vigilance du même nom, camoufle une entreprise de destruction massive contre laquelle il est urgent de se dresser : celle de l’éducation.
En conséquence, si l’on comprend difficilement ce qui pourrait justifier la prolongation d’un état d’urgence sanitaire, on souscrit en revanche sans réserve à un état d’urgence de l’école comme de l’hôpital, deux zones désormais sinistrées.
On nous avait prévenus : « Nous sommes en guerre, en guerre contre un ennemi invisible. » Cette guerre des mots, des idées, de la parole libre et éclairée brutalise les Corps forcément, menace de les disloquer.
Voici donc un nouvel appel à une résistance active, un appel à « faire corps » pour « faire sens » puisqu’il est urgent de protéger une discipline qu’à force de regarder agoniser, on va finir pour mettre en bière, mais cette fois sans l’humour et le talent tant regretté du groupe Bourbaki au moment de la publication de leur inoubliable faire-part de décès. Un canular à lire, à relire absolument alors que quelques mois à peine nous séparent de l’édition de « Récoltes et Semailles » d’A. Grothendieck annoncée chez Gallimard pour janvier 2022.
Cette tribune militante, engagée sans doute, n’a pas la prétention d’être exhaustive ; d’autres avant et avec moi se sont inquiétés de la tentation d’une forme de désinstruction, voire de déconstruction des savoirs et des êtres. Il s’agit avant tout d’une invitation aux enseignants, notamment issus de l’éducation nationale, à se mobiliser tout d’abord contre l’aberration d’une épreuve de spécialité prévue au mois de mars qui empêche d’aborder sereinement et de manière équilibrée, motivée aussi, les différentes parties d’un programme aussi hétérogène qu’ambitieux. Cette échéance doit être repoussée au mois de mai au plus tôt. Enseigner n’est pas associable à un processus de gavage, car d’un gavage, on ressort écoeuré, mais certainement pas instruit.
Parce que le temps presse, les profs doivent absolument sortir de leur mutisme et s’emparer à voix haute du débat, l’alimenter de sorte de construire une réflexion étoffée en plus d’un plaidoyer argumenté pour un enseignement de qualité, à la mesure tout simplement de celui que l’on a parfois eu la chance de recevoir et que l’on souhaite légitimement, à notre tour, dispenser. Je compte donc sur l’APMEP 1 et sur la SMF 2 dont on connaît l’engagement, pour soutenir cette requête.
Il conviendra aussi dans un second temps de se pencher sur la pertinence desdits programmes, notamment dans le cadre du lycée. Comme d’autres j’imagine, je serais curieuse de comprendre ce qui a pu motiver en terminale, la réintégration d’un chapitre sur les méthodes de dénombrement quand cet outil n’est finalement pas appliqué aux calculs des probabilités (ou si peu, avec la loi binomiale enseignée en classe de première il y a de cela deux ans). Pourquoi et comment a-t-on pu estimer que le chapitre pourtant fondamental des nombres complexes n’avait plus sa place dans le socle de spécialité, mais seulement dans le cadre de l’option facultative des maths dites « expertes ? » Pourquoi avoir réintroduit la notion d’équations différentielles du premier ordre, ce qui laisserait penser à une orientation vers des outils de maths appliquées, pour se séparer dans le même temps des lois continues dont l’étude de la loi normale si présente en médecine et en économie (cette loi associée à la fameuse courbe en cloche, la gaussienne, désormais si familière aux Français, covid oblige) ? Pourquoi lui avoir préféré l’inégalité de Bienaymé-Tchebychev, un outil difficile à appréhender si bien que l’on se retrouve réduit à des applications naïves qui produisent des résultats qui le sont tout autant avec des majorations souvent grossières ? S’il y a dans ces choix une motivation pédagogique, je ne la comprends pas. Que les enseignants des classes préparatoires notamment, ces observateurs en première ligne, n’hésitent pas à nous communiquer leur ressenti ainsi que les universitaires dont les retours sont encore trop timides.
André Revuz, dans les années 80, se posait déjà une question qui allait devenir le titre d’un magnifique ouvrage d’une intelligence et d’une pertinence intemporelle et qui forcent l’admiration, question plus que jamais d’actualité : « Est-il impossible d’enseigner les maths ? »
Avait-il seulement imaginé que cette discipline serait un jour considérée comme secondaire et reléguée sans émotion au rang d’option, les si mal nommées : « spécialités » ? Nous y reviendrons.
On est à un moment charnière, précipité par une réforme tellement aberrante qu’elle en serait presque risible si les conséquences n’étaient pas dramatiques ; un moment où l’on se demande si les maths ont encore un avenir en France ou si l’on finira par simplement les tolérer en les associant aux caprices de quelques originaux parqués au fond d’un couloir. À moins qu’on ne les réduise à des compétences strictement numériques, les maths « utiles » du digital. Depuis quelques mois d’ailleurs, elles sont trop souvent réduites voire assimilées aux entreprises, à bien des titres contestables, de modélisation. Un point de vue pour le moins réducteur.
Bien entendu, chaque début d’année est l’occasion de dresser un cahier de doléances pour ne pas dire de lamentations face aux dommages causés par un été mathématiquement meurtrier. Mais pour travailler avec des élèves de première et de terminale essentiellement depuis plus de quinze ans dans des contextes variés, force est de constater que je n’ai jamais observé avec cette intensité, une telle détresse en matière de compréhension, et ce, que les élèves soient issus de lycées privés réputés prestigieux ou de structures publiques ; c’est à dire qu’ils aient été soumis ou pas l’an dernier à ce régime absurde en plus d’être inégalitaire, de demi-jauge.
On a désormais le sentiment douloureux d’être réduits à dispenser un enseignement d’urgence, quelque chose comme les premiers secours pour parer au plus pressé en évitant l’hémorragie fatale à quelques heures du devoir surveillé, mais rien de réellement abouti qui garantirait la satisfaction d’un travail bien fait, c’est-à-dire, durable. À cette urgence, est associée une forme de maltraitance, au sens littéral de : « traiter mal, » qu’il s’agisse des élèves ou de la discipline avec un corollaire immédiat : le mal-être, la culpabilité de l’enseignant. Donc non, la fuite des profs ne saurait être réduite à des arguments strictement comptables que l’on pourrait imaginer juguler par une simple augmentation de salaire. Le malaise, puisqu’il existe, est bien plus profond et plus dense. Il faudra un jour comprendre que l’on ne peut pas tout chiffrer. Alors bien sûr, on dit : « le temps, c’est de l’argent » ; si la réciproque est vraie, alors les profs ont besoin d’argent parce qu’ils ont besoin de temps et les élèves aussi.
Il faut bien avouer que prof de maths est désormais sur un siège éjectable, car sa discipline a été reconnue, décrétée, « non essentielle » si l’on se réfère à un vocabulaire qui nous est désormais familier. Il n’a plus d’autres choix pour attirer les élèves dans son cours et surtout les convaincre de rester, que de se transformer en une sorte de VRP et de consentir par la même occasion à un certain nombre de concessions quitte à s’arranger un peu avec la réalité pour la rendre plus attractive, plus « vendeuse » (on pense aux notes largement ajustées, au programme libre d’interprétation).
Dans le lycée start-up de Blanquer, le client-élève est roi et il le sait. Concrètement, « maths expertes » ou « matelas-confort », même combat. Vous essayez le produit durant 30 jours et s’il ne vous convient pas, vous avez jusqu’au 30 novembre pour vous désister après acceptation de votre requête auprès du proviseur. Une formalité si j’en crois mon expérience. « Satisfait ou remboursé » en quelque sorte. Certains en rêvaient, Blanquer l’a fait. L’élève est désormais un consommateur en fin de chaîne, encouragé à choisir ses options par opportunisme, c’est-à-dire en en évaluant la rentabilité notamment au regard du redoutable et insondable Parcoursup, le côté décidément obscur de la force. À la manière du gouvernement, le jeune gère un risque, un risque seulement d’une autre nature que pénal. Pour le moment…
Il serait trop long de revenir sur l’imposture du Grand Oral qui a été dénoncée à de nombreuses reprises par des collègues de philosophie notamment ; en réalité, le simple nom un peu trop « ronflant » de ce simulacre d’épreuve suscite naturellement inquiétude et méfiance. Il s’agit du bac option « force de vente » à tous les étages ; on teste durant quelques minutes l’éloquence de l’élève, paraît-il, ou plutôt sa capacité à faire un peu de tout avec beaucoup de rien.
Pendant que ce temps commercial s’écoule lentement, on est face à un illettrisme mathématique grandissant. Les lacunes ont atteint un tel seuil dans une discipline qui se construit par strates, une discipline faite de correspondances que l’on sort de cours presque hagard tant il faut déployer d’énergie pour tenter de donner ne serait-ce qu’un peu de recul aux élèves, espérant ainsi les soulager. On a toujours dans un coin de la tête cette phrase de Nicolas Boileau : « Ce qui se conçoit bien s’énonce clairement ». Reste que l’on ne parvient notamment plus en terminale à convaincre nos jeunes que les questions d’un exercice sont autant de bribes, autant de personnages d’une histoire dont il s’agit simplement de respecter le déroulement, le fil conducteur. Que les questions ne sont ni gratuites ni indépendantes en général. Qu’il faut se saisir du : « en déduire » qui débute une phrase parce qu’il est en soi une partie de la réponse à venir et qu’il est primordial de se saisir de ce tremplin…
Parce qu’ils ne savent plus vraiment lire, plus vraiment écrire non plus et qu’ils n’ont plus de connecteurs logiques à leur disposition, les élèves sont trop souvent incapables de construire un raisonnement indépendant et argumenté. On parvient tout au plus à déclencher chez eux des réflexes, des automatismes régis par les circuits courts de la récompense, à grand renfort d’exercices types qu’ils reproduisent inlassablement sans passion et sans haine, mais surtout, sans jamais aiguiser leur esprit critique. C’est pour nous, enseignants, les prémisses de l’échec.
Mais qu’importe finalement puisqu’à chaque élève, on est juste tenus d’associer un camembert (un diagramme circulaire, retour dans le monde merveilleux de marketing) qui rend compte d’un coup d’œil (code couleur oblige) des acquis et des faiblesses suivant les séquences.
C’est bien là ce que l’on nous présente, avec l’introduction des neurosciences à l’école couplées à la troublante « pédagogie inversée, » comme la Rolls-Royce de l’enseignement : le fameux enseignement personnalisé, celui des capsules et des bilans de compétences. Celui des profils et des pronostics aussi.
Il faut bien comprendre qu’en maths, on est dépendants de la maîtrise de la langue ; c’est une discipline d’expression avec sa ponctuation et sa grammaire. Une langue pour nous tous (ou presque) étrangère bien sûr, mais qu’à force de pratiquer, on a des chances de parler assez correctement. Suffisamment en tout cas, pour se faire comprendre et être compris en retour. Toujours est-il que l’on a besoin du : « mais, ou, et, donc, or, ni, car » si cher au primaire et aux exercices de Bled de mon enfance. Ce sont ces mots « minuscules » qui permettent d’articuler le raisonnement, en lui donnant sa cohérence et sa consistance.
Dans une phrase mathématique, il y a une action, une sorte de verbe (=, ≤, ≥, 6= ) que la plupart des élèves ne repèrent plus si bien que l’on est sans cesse contraints, tentés, de reformuler les questions pour qu’ils parviennent enfin à se les approprier. Si seulement ils cherchaient à comprendre plutôt qu’à reconnaître, plutôt qu’à se souvenir… Si seulement, ils osaient de nouveau prendre leur raisonnement en main.
Les mots qui devraient tant les aider à se repérer, à se raccrocher, les déroutent au contraire. Je prends souvent l’exemple des suites auxiliaires, ces suites au service d’une suite-mère dont l’étude pose quelques problèmes puisqu’elle ne tombe pas sous la coupe des suites simples à savoir, les suites arithmétiques ou géométriques. Comment est-il possible que le parallèle pourtant naturel avec une auxiliaire de vie qui vient vous seconder dans les tâches quotidiennes ne les aide pas à comprendre la philosophie de ce type d’énoncés ?
Autre exemple, la relation de Chasles rapidement évoquée dans les prémisses du chapitre de géométrie dans l’espace avec la notion de vecteurs coplanaires. Là encore, quand on évoque, pour les aider à s’approprier la notion, les mots de : « copropriété, codirection, colocation », ils vous rétorquent qu’ils ne voient pas le rapport ! J’ai des terminales, assez brillants au demeurant, qui m’écrivent tranquillement, pas une fois, mais bien à dix reprises :
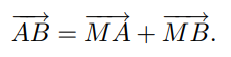
Je rappelle que cet outil très intuitif était au programme du brevet des collèges il y a encore une dizaine d’années. Quand vous leur dites : « Donc si tu fais le trajet Antibes-Bordeaux, tu penses que tu pars de Marseille ou bien que tu peux faire, si tu le souhaites, une escale à Marseille ? » Et le gamin de répondre : « vu comme çà c’est évident, mais d’habitude, les maths ne veulent rien dire donc… »
Ce matin encore, pour prouver que trois points de l’espace formaient un plan, j’ai un élève qui envisageait de prouver que ces derniers étaient coplanaires. Pour plaisanter un peu, je lui demande alors : « je voudrais bien que tu me prouves s’il te plaît que les points A et B sont alignés… !
Les maths pour cette génération, ça ne se comprend pas ; ça se retient et encore, pas longtemps. C’est un peu magique finalement ; il faut avoir un don, être fait pour ça comme ils disent. Quand on ne comprend pas, c’est la fatalité en quelque sorte et on n’y peut rien !
Les outils fondamentaux normalement vus au collège ne sont plus jamais acquis ; qu’il s’agisse des fractions, des propriétés des puissances, de celles des racines carrées ou encore de la factorisation, sans parler des identités remarquables devenues une exigence digne de Normale Sup à écouter les élèves. On paie au prix fort l’application aux maths d’une sorte de méthode globale au lieu d’avoir conservé la bonne vieille méthode syllabique basée sur la compréhension.
Ils retiennent que diviser par 0, 1 revient à multiplier par 10, mais ils ne savent pas pourquoi. Ce qui est grave, c’est que de ne pas comprendre ne leur manque pas ou plus. Ils délèguent aussi facilement qu’ils abdiquent et s’en remettent malheureusement complètement à nous. Il faudrait “les repousser” d’une certaine manière pour leur rendre leur autonomie. On rencontre des erreurs réellement grossières qu’ils devraient être en mesure de corriger d’eux-mêmes, simplement via des arguments de bon sens dont ils sont largement capables. Mais pour cela, il faudrait encore qu’ils acceptent de s’immerger dans les énoncés.
Ci-dessous, une galerie d’art non soumise au pass sanitaire ; une sorte de chambre des curiosités extraite de mon, de notre quotidien. “Parce qu’il faut rire de tout avant que d’en pleurer”, que mes élèves soient chaleureusement remerciés pour leur extraordinaire… créativité :
Or la concentration est désormais vécue comme une sorte de vertige, de saut dans l’inconnu ; elle revêt un caractère inquiétant même, car elle semble avoir pour but de les isoler, de les éloigner de leur tribu. Combien de notifications loupées pendant que je planchais sur cet exercice ? On retrouve ici la fameuse balance : “bénéfices/risques.”
C’est ainsi que ce temps consacré à la réflexion, ce temps “calme” bien plus que “mort”, est associé à du temps perdu. En première, puisque j’évoque les fractions, j’ai vu en septembre le “calcul” suivant :
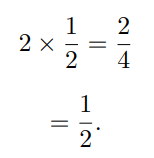
Pour cet élève de seize ans, tout à fait standard au demeurant, quand vous avez deux moitiés de pomme, vous avez… une demi-pomme. Et oui. Pas besoin des neurosciences pour comprendre que chez certains élèves, le 2 de x = 2 n’est pas le 2 de “deux pommes”.
Pour ne rien arranger, il y a chez cette génération une addiction aux raccourcis, une dépendance à l’immédiateté que l’on a, sinon crée, du moins entretenue à grand renfort de QCM. Cette manière synthétique et très artificielle d’évaluer les élèves contre laquelle je ne cesse de m’insurger, a pour conséquence qu’il est désormais nécessaire de déployer les grands moyens pour restaurer l’envie d’une rédaction soigneuse, rigoureuse et précise. Le déconditionnement est assez douloureux en plus d’être incertain.
Les explications, estimées fleuves, les étouffent. “TROP DE MOTS”, disent-ils. Ou encore : “Il faut vraiment écrire tout çà ?” en espérant négocier une remise de peine d’une ligne ou deux. Il faut d’ailleurs reconnaître que lorsqu’ils communiquent entre eux ou avec nous par messages, ils en décuplent le nombre comme s’il était désormais nécessaire pour assimiler une information ou bien la transmettre, de la démembrer, de la disséquer.
Ce qui est incohérent, voire paradoxal, c’est que ces mêmes élèves rétifs aux phrases sont souvent terriblement réfractaires au langage algorithmique qui aurait a priori tout pour les séduire. Était-il donc si urgent d’investir (je n’ose pas dire : “contaminer”) le cours de maths par des séances de Python quand la plupart des élèves ne connaissent ni le sens du mot “hypothèse” ni celui du mot “conjecture” à presque 18 ans ? Rien n’est moins sûr.
On constate enfin une résistance à l’effort très dégradée et en même temps une forme de crédulité, de passivité surtout, teintée d’indifférence qui doit nous alerter, car notre but est bien de participer à l’émancipation intellectuelle de ces jeunes. On ne souhaite en faire des matheux à tout prix, mais seulement des citoyens libres, capables si besoin de démonter, de repérer un argumentaire fallacieux. Ils assistent trop souvent au cours en zombie, réduits à l’état de scribes. J’ai en tête un exemple récent d’un élève de terminale dont je consultais le cahier de cours et notamment le chapitre concernant les limites de suites. Au moment de produire les énoncés relatifs aux théorèmes des “Gendarmes” et de comparaison, je me rends compte que le lycéen, parce qu’il y voyait mal au tableau, avait remplacé tous les termes vn par √n !!!! Comment peut-on en arriver à un tel degré d’incompréhension alors qu’il s’agit là encore d’énoncés très intuitifs (jusqu’au nom qui est très imagé et ne fait d’ailleurs pas l’unanimité). Il s’agit aussi de les déconditionner de l’ambiance délétère des derniers mois qui, sans état d’âme, a associé le doute nécessaire, le doute légitime, à une forme de complotisme.
Pour clore ce long, trop long billet, je vais suivre la voie de l’humour, celle de la dérision en même temps que les conseils d’une amie cancérologue qui m’encourage toujours à témoigner, à revenir à des cas concrets. “C’est ce qui intéresse les gens”, me dit-elle.
Faute de témoignages pertinents, je vais entreprendre en revanche de rassurer les jeunes collègues qui n’auraient pas été aussi attentifs que nécessaire lors des précieux cours dispensés à l’INSPE (autrefois, l’IUFM) pour gérer au mieux une classe. Ne vous inquiétez pas ; rien n’est perdu, bien au contraire, car nous disposons grâce à ce gouvernement, cet État-care bien décidé à combler nos moindres désirs et à anticiper chacune de nos inquiétudes, de séances de travaux pratiques hebdomadaires.
J’ai nommé : les séances à l’Assemblée Nationale avec un maître de stage incontesté, que le monde entier nous envie : Olivier Véran. On pourra se reporter aux séances hautement instructives des 19 et 20 octobre 2021. Première règle : jauger (voire juger ; l’œil acéré d’un neurologue aide bien sûr) l’auditoire. Autrement dit, intégrer le douloureux principe de réalité selon lequel cette année encore, vous n’êtes pas face à des lumières. Oh que non… ! Mais que voulez-vous ? Chacun sa croix.
Ne pas hésiter à parcourir l’amphi, fût-il clairsemé, d’un regard oscillant entre résignation, suffisance et accablement avant de se lancer dans l’arène,
fougueusement en entreprenant un monologue aussi inintelligible que possible, ce qui nécessite une élocution assez rapide en plus d’une aptitude à l’apnée que vous seriez bien inspirés de développer. Le but est d’éviter au maximum les questions. Que l’adhésion à vos propos soit par la suite extorquée ou consentie, peu importe. On ne va pas jouer sur les mots/maux.
Malheureusement, il y a dans toutes les classes des élèves terriblement lents comme ce député, peu coutumier d’internet, qui ne parvenait pas à trouver sur le site de l’agence européenne du médicament, la description et le report des effets secondaires incombables au vaccin (vaccin dans un sens à préciser, puisque “non pasteurien”). Mais il faut aussi et surtout compter avec les fortes têtes du type F. Ruffin, la réincarnation du redouté élève Ducobu bien connu des bédéphiles. Toujours au fond de la classe, tripotant son masque et adepte d’un humour douteux, avec des questions plein le cartable et qui n’en finit pas de discuter avec son voisin alors même que le prof s’exprime. Bref, cet élève, c’est votre défi. Vous noterez en conséquence, avant de vous en inspirer bien sûr, l’agilité et l’extrême patience dont on a fait preuve O. Véran face à cet élément perturbateur. On peut même parler de bienveillance, ce mot devenu un concept, si cher à J. M. Blanquer. Toujours très pédagogue, serein même, le ministre de la Santé et des Solidarités (et oui, on ne s’y fait pas…) l’a gentiment rappelé à l’ordre en prenant soin de préciser qu’il ne répéterait pas l’explication en cas de récidive.
Il n’y a pas à dire : “une main de fer dans un gant de velours”… Une main de fer surtout. Car c’est çà la réalité et “si vous ne voulez pas l’entendre, sortez d’ici.”
En attendant, restons groupés. “L’orage aussi peut conduire au port” disait Jean-François Senault alors gardons espoir.
Karen Brandin
⚠ Les points de vue exprimés dans l’article ne sont pas nécessairement partagés par les (autres) auteurs et contributeurs du site Nouveau Monde.