03/12/2021 (2021-12-03)
[Source : lachainehumaine.com]
Par Pierre Lecot, de la chaîne « Décoder l’éco »
La mortalité hivernale est-elle vraiment un phénomène de propagation virale ?
1. L’importance de standardiser les décès pour prendre en compte l’augmentation et le vieillissement de la population
La France vieillit. Par conséquent, le nombre de morts chaque année augmente naturellement depuis 2010 (Figure 1). Cette hausse du nombre de décès n’est pas le signe que la santé des Français se dégrade, mais uniquement le résultat de l’augmentation du nombre de personnes âgées. En effet, à force de vieillir, tous les humains finissent par mourir.
Figure 1 : Décès annuels en France
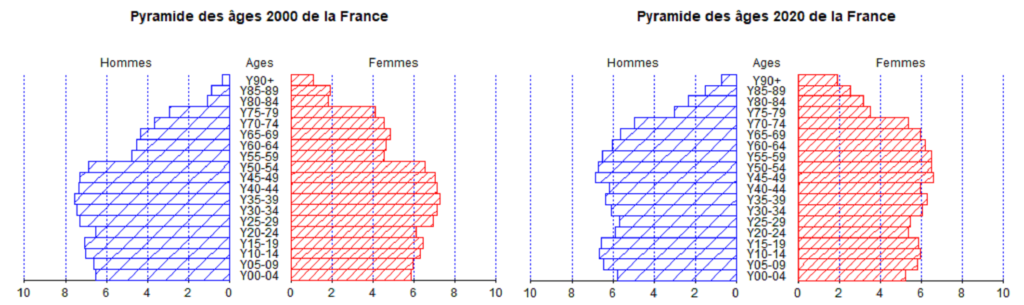
Le vieillissement français s’illustre par l’évolution de la pyramide des âges de la France entre 2000 et 2020, réalisée avec les données disponibles sur Eurostat (Figure 2). En 20 ans, la génération des baby-boomers est, logiquement, passée de la tranche des moins de 55 ans à celle des plus de 65 ans. Dès lors, il est tout à fait normal que le nombre de décès en France augmente chaque année, et cela va continuer à augmenter pendant encore au moins 20 ans, jusqu’à ce que le gros de cette génération ait décédé.
Figure 2 : Pyramide des âges de la France en 2000 et 2020
Ainsi, il ne faut jamais commenter des nombres de décès bruts qui augmentent ou baissent non pas selon l’arrivée des maladies, mais toujours selon la taille de la population et selon l’âge des personnes. En effet, s’il y a plus de décès en France qu’au Luxembourg, c’est parce que les Français sont 100 fois plus nombreux que les Luxembourgeois. S’il y a plus de décès dans un EHPAD de 200 personnes que dans une école maternelle de 200 enfants, ce n’est pas parce que l’EHPAD est plus dangereux que l’école maternelle, mais uniquement parce que les résidents d’un EHPAD sont beaucoup plus vieux que les élèves d’une école maternelle. Ainsi, comparer des nombres de décès entre 2 populations ne peut pas se faire avec les seuls chiffres bruts, mais toujours en corrigeant de la taille de la population, et aussi en corrigeant de l’âge des gens. Il s’agit de standardiser les décès pour mettre la même population partout (Figure 3). Standardiser les populations pour comparer les décès est le calcul reconnu par Eurostat1 ou l’OMS.2 L’office statistique Ecossais en a détaillé les intérêts3 et compare les résultats des mortalités au regard des standardisations de 1976 et de 2013.
Figure 3 : Formule de la standardisation des décès
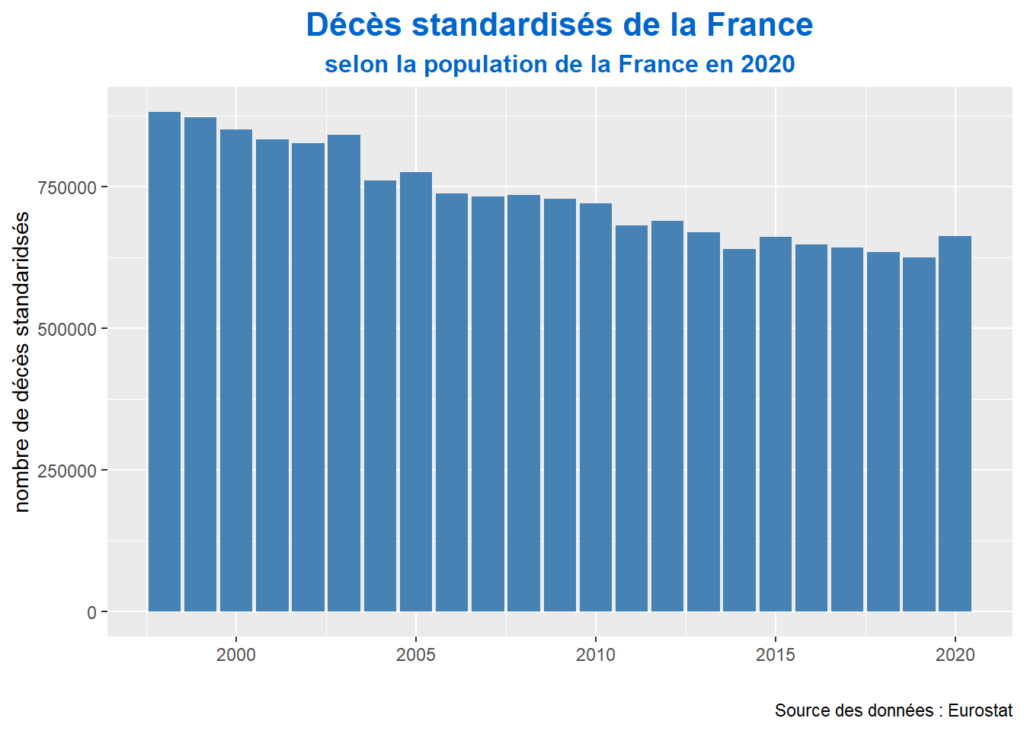
Pour comparer le nombre de décès en France de ces dernières années avec l’année 2020, nous avons standardisé les décès, en appliquant la population par âge de 2020 à toutes les années du passé. Il en est ressorti que l’année 2020 n’est pas du tout une année de record de mortalité (Figure 4).
Figure 4 : Décès standardisés en France selon l’année 2020
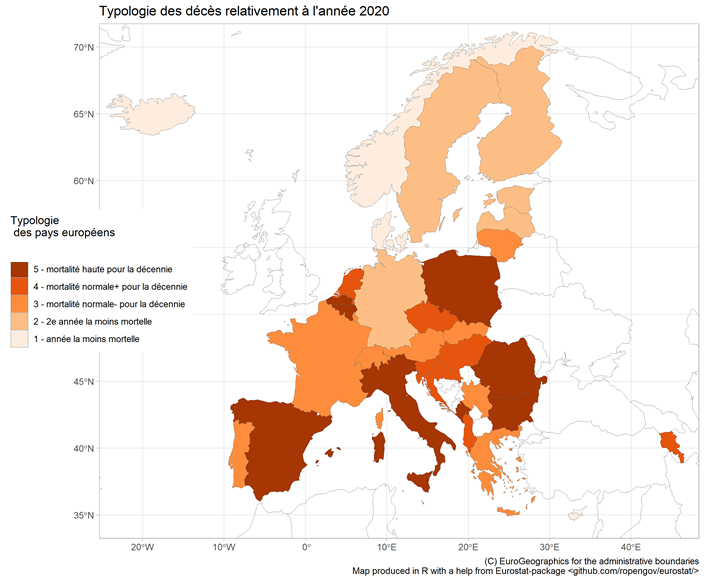
L’année 2020 est au niveau de l’année 2015. Il s’agit de la 6e année la moins mortelle de toute l’histoire de la France. Cette situation est la même quel que soit le pays en Européen considéré.4 Pour certains pays, comme la Norvège ou l’Islande, l’année 2020 est un record absolu de sous-mortalité. Au pire l’année 2020 présente une mortalité haute relativement à la décennie, mais plus basse que n’importe quelle année précédente comme pour la Belgique ou l’Espagne (Figure 5).
Figure 5 : Typologie des pays européens selon le rang dans l’histoire des décès standardisés de l’année 2020
2. Des cycles annuels de hausse et baisse de mortalité
L’étude des décès hebdomadaires standardisés en France depuis 2013 nous permet de visualiser les cycles de mortalité (Figure 6). Chaque année, le nombre de décès augmente en hiver et diminue en été. Cette augmentation de décès l’hiver est concomitante des maladies hivernales. Parmi elles, les infections respiratoires aiguës peuvent être attribuées à des virus comme les grippes, les rhinovirus ou les coronavirus, ou à des bactéries comme les pneumocoques, les staphylocoques, Haemophilus influenzae ou d’autres.
Figure 6 : Décès hebdomadaires en France standardisés selon 2020
Il est important de faire la distinction entre l’origine et le symptôme. Jusqu’en 2019, les déclarations d’infections respiratoires hivernales faisaient mention d’un « état grippal » du patient. Ainsi, jusqu’à récemment, la surmortalité hivernale était comptabilisée comme étant causée par les virus de la grippe, justifiant notamment la politique vaccinale.
Certains hivers présentent des pics de mortalité nettement supérieurs à d’autres. L’hiver 2013-2014 a connu des pics de mortalité bien moins élevés que l’hiver 2014-2015. Cette différence fait partie des éléments expliquant les différences de décès d’une année sur l’autre. Nous avons déjà détaillé ce phénomène dans d’autres communications. Une explication serait le principe des années moissons.5 Les hivers doux et peu mortels laisseraient en vie les plus fragiles de la population et ces derniers décéderaient pendant les hivers plus rudes. L’année suivante compterait mécaniquement moins de décès faute de personnes fragiles.
Une théorie concernant la hausse de mortalité hivernale est la propagation virale. Il s’agit de dire que l’hiver les virus arriveraient de l’extérieur et circuleraient dans la population. Cette théorie a été modélisée au début de 20e siècle6 avec les premiers modèles de propagation épidémique. Le fameux modèle SIR7 a été construit en traduisant mathématiquement cette théorie. Il contient plusieurs paramètres qui définissent les fameux R0, Rt et Reff. Cette hypothèse de propagation virale sert de socle à un certain nombre des politiques de santé publique. Elle permet notamment de justifier la politique vaccinale antigrippe et est donc naturellement défendue par les industriels pharmaceutiques qui en sont les bénéficiaires directs. Il existe aujourd’hui bien d’autres modèles de propagation épidémique. Cependant le seul modèle médiatisé et utilisé par les gouvernements (retrouvé dans des documents fournis au Sénat8 ou au sein des discussions de l’assemblé9) pour justifier les politiques coercitives est celui de la propagation exponentielle. Cette propagation exponentielle entraînera alors une augmentation exponentielle de recours à l’hôpital (la part des contaminations qui dégénère) et une augmentation exponentielle des décès (la part des formes graves qui sont fatales).
Dans tout l’éventail imaginable des principes de propagation, une démarche simple de confirmation ou d’infirmation de la théorie extrême utilisée actuellement est de la confronter à son autre extrême. La vérité n’est certainement pas contenue dans un de ces 2 points trop simplistes, mais les statistiques peuvent nous permettre d’avoir une idée duquel de ces 2 points la réalité se rapproche.
Si nous récapitulons nous avons donc l’hypothèse A suivante :
Les hausses de mortalité, notamment hivernales, sont dues à la propagation exponentielle de maladies (notamment virales) au sein de la population.
Cette hypothèse a des implications très forte sur la politique de santé :
• Les humains sont tenus responsables de l’état de santé de leurs voisins (contaminations) et légitime les pratiques de quarantaine, isolement, port du masque etc.
• Elle légitime la stratégie de lutte préventive contre les pathogènes circulant (vaccination antigrippale)
Nous allons la confronter à l’hypothèse B :
Les hausses de mortalité, notamment hivernales, sont dues aux conditions extérieures et à la dégradation de l’état de santé général.
Cette hypothèse change les priorités de la politique de santé :
• Les humains ne sont pas tenus responsables de l’état de santé de leurs voisins. Il n’y a alors aucune raison de mettre en place des politiques restrictives
• La stratégie préventive devient une stratégie de santé générale (sport, alimentation, sorties, éventuellement apports vitaminés, qualité de l’air)
On note que l’hypothèse A sert de justification aux mesures coercitives gouvernementales et légitime la privatisation de la santé par des industriels qui vendent (ou forcent l’achat par l’intermédiaires des gouvernements) des vaccins et autres produits préventifs.
L’hypothèse B ne permet pas de politiques de coercition de masse. Elle soutiendrait des politiques préventives peu onéreuses, individualisées, sans promesse de vie éternelle, mais avec des améliorations de qualité de vie.
3. Les indices à notre disposition
3.1. Les indices à notre disposition : l’absence d’exponentielle
Si on suppose que l’hypothèse A est vraie, alors des phénomènes de vagues de propagation devraient être visibles à l’échelle européenne ou au sein d’un même pays. Cependant on observe l’inverse.
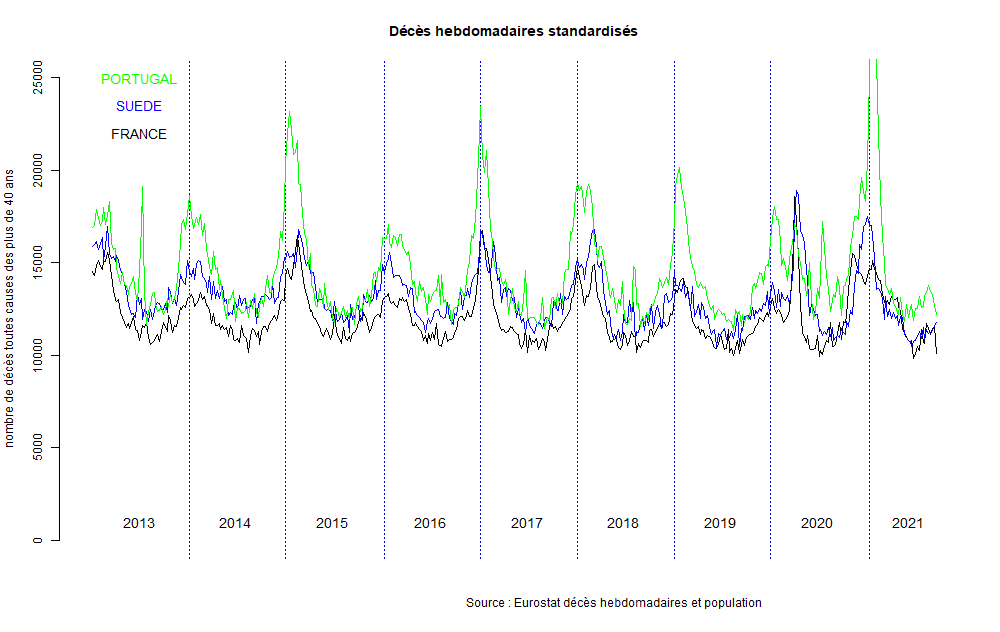
Ce phénomène de hausse de mortalité hivernale est complètement simultané sur toute l’Europe (Figure 7). La standardisation des décès nous permet de représenter les différents pays et années sur un même graphique. Ici toutes les populations sont ramenées à la population française de 2020.
Figure 7 : Décès standardisés France, Portugal, Suède, selon 2020
De la Suède jusqu’au Portugal, les hausses de mortalité sont naturellement simultanées tous les hivers, et même les étés lors des épisodes caniculaires. La mortalité hivernale des pays européens n’est donc pas en lien avec un phénomène de diffusion de maladies l’hiver en Europe. Le Portugal et la Suède sont séparés par 3 000 km. Si la diffusion entre individus de maladies l’hiver était responsable de l’augmentation de la mortalité, des décalages temporels devraient être visibles, ce qui n’est pas le cas. L’augmentation des décès ne représente pas le déplacement des maladies, mais leur apparition partout à la fois. Il s’agit d’une manifestation de la dégradation cyclique de l’état de santé. Cette dégradation simultanée partout en Europe se traduit par l’apparition de symptômes attribués à des maladies hivernales et par l’augmentation des décès. Le phénomène de courbe en cloche concernant la mortalité n’est pas le résultat d’un phénomène de propagation, mais d’un phénomène d’apparition. Il est évident que les portugais ne contaminent pas les suédois, ni inversement.
Le même résultat se constate à des niveaux plus fins que les pays. En France, pour lequel nous avons des résultats départementaux, les pics de mortalité sont synchronisés. Ils sont plus ou moins visibles selon l’âge et la taille de la population.
On a ici un fort indice de rejet de l’hypothèse A. Il nous manque un élément explicatif pour nous diriger vers l’hypothèse B.
3.2. Les indices à notre disposition : l’absence d’exponentielle
Il est important de rappeler que c’est directement à cause du modèle de propagation utilisé qu’existe le discours sur l’augmentation exponentielle des malades et des décès. En effet, les équations des modèles de propagation se résolvent grâce aux fonctions exponentielles. Ainsi il ne s’agit pas d’une observation, mais directement du modèle lui-même. Ce n’est donc pas une réalité vérifiée, mais un présupposé basé sur une construction de l’esprit. En téléchargeant la série longue des décès quotidiens de l’Insee,10 nous pouvons observer les variations de décès depuis 50 ans (Figure 8).
Figure 8 : Décès quotidiens français lissés sur 7 jours depuis 1968
Les données sont lissées sur 7 jours de façon à éviter le biais induit par le jour de déclaration de décès. En effet, en France, on constate peu de décès déclarés les samedis et dimanches. Cela a plus de raisons d’être dû à un moindre nombre de constats de décès par les médecins qui sont moins nombreux à être actifs ces jours-là, plutôt qu’à une réelle protection dominicale.
Ainsi en France, depuis 50 ans, les hivers sont des périodes de forte hausse de mortalité. L’année 2020 est bien visible avec la particularité d’avoir des périodes décalées, mais également la fin de l’année 1969 dont la mortalité hivernale a été attribuée à la célèbre « grippe de Hong-Kong ». Certains étés sont aussi particulièrement mortels, avec notamment la canicule de 2003 (mais également les canicules de 1975, 1976 et 1983 non représentées ici). On note ainsi que les épisodes caniculaires ne sont pas récents et sont observables depuis le début des données modernes. L’année 2003 est exceptionnelle surtout par le nombre de personnes âgées qui étaient en vie à cette période (contrairement aux années 1975,1976 et 1983).
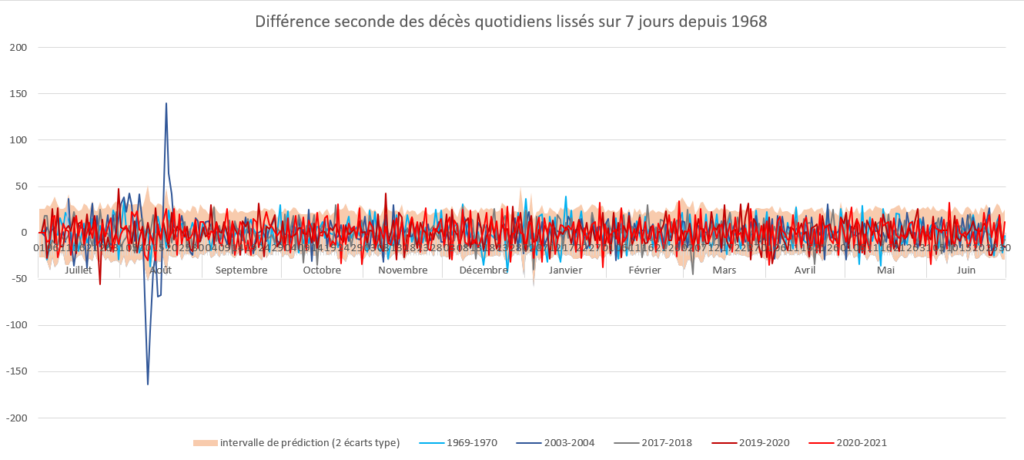
Il est facile de vérifier si des augmentations exponentielles de mortalité ont déjà eu lieu depuis 50 ans en France. Une des propriétés de l’exponentielle est que sa dérivée est une exponentielle. Ainsi, si le nombre de décès augmente de manière exponentielle, alors le nombre de décès accélère également de manière exponentielle. Pour vérifier si un tel évènement existe, il suffit de calculer l’accélération des décès d’un jour à l’autre, en calculant la différence seconde (Figure 9).
Figure 9 : Différence seconde des décès quotidiens lissés sur 7 jours depuis 1968
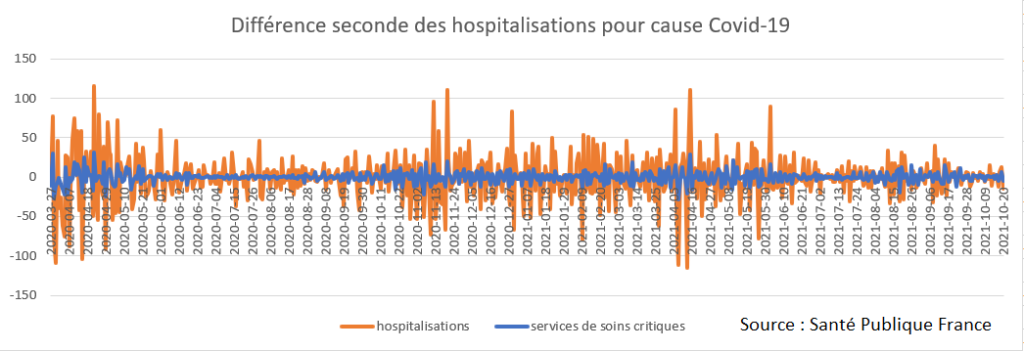
Figure 10 : Différence seconde des entrées à l’hôpital
et en service de réanimation pour Covid-19
A ce stade, le modèle de propagation ne peut prétendre à une validation par l’observation. Nous sommes dans le cas où la théorie a pris possession de notre évaluation de la réalité. Il est tout à fait possible de calculer pour chaque hiver, ou même sur chaque canicule, une courbe de propagation SIR. Il suffit d’ajuster les différents paramètres pour que la courbe colle au plus près de la réalité. La folie, c’est de prétendre que d’avoir fait coller une courbe à la réalité montre qu’on a compris le phénomène. La folie c’est d’utiliser les paramètres pour ensuite calculer le R0 et s’en servir pour imposer des décisions politiques.
3.3. Les indices à notre disposition : le lien parfait entre décès et température extérieure
Météo France met à notre disposition depuis janvier 2021 des jeux de données sur les relevés météorologiques.11 Des données de températures, d’humidité, de pression atmosphérique, sont disponibles en de nombreux points et jusqu’à 25 ans de profondeur. Les données de température sont les plus nombreuses et les plus fiables. Elles couvrent de nombreux espaces et territoires.
Les conditions météorologiques extérieures sont toutes liées entre elles. La température basse de l’hiver est souvent liée à un assèchement de l’air et des basses pressions atmosphériques. La température extérieure est donc vue ici comme un indicateur de relevé météorologique. Il ne s’agit pas de supposer ou conclure que la température extérieure tue les gens, mais bien de savoir si les conditions météorologiques quelles qu’elles soient ont un impact sur la mortalité.
Pour cette analyse, le taux de mortalité par âge chaque jour en France sur chaque département est apparié à la température moyenne extérieure ce même jour sur ce département.
Nous allons donc pouvoir observer le lien entre mortalité et température extérieure. Les années 2017, 2018 et 2019 sont observées ici de façon à ne pas être perturbé par la Covid-19 et les mesures prises. Les décès sont lissés sur 7 jours pour la même raison que précédemment. Ils sont décalés de 5 jours par rapport à la température en considérant que le décès n’est pas immédiat, mais suit un état de dégradation progressive appelé maladie.
Le test de corrélation de Spearman12 nous permet de savoir si les taux de mortalité et les températures évoluent en même temps. Ce test compare les rangs entre les points de chaque variable. Il a l’avantage de ne pas supposer la nature de la relation entre les 2 variables. Il mesure si la relation entre les 2 variables est monotone. La corrélation d’après Spearman est parfaite lorsque le Rhô vaut 1 ou -1 (Figure 11). Il vaut 1 lorsque les maximas des deux variables sont synchronisés et vaut -1 lorsque chaque maximum de la première variable correspond à un minimum de l’autre variable.
Figure 11 : Exemple de corrélation parfaite de Spearman
A l’inverse, le Rhô vaut 0 lorsqu’il n’y a pas de relation monotone ente les 2 variables (Figure 12).
Figure 12 : Exemple d’absence de corrélation selon Spearman
Pour simplifier la lecture visuelle, la température est inversée car les décès augmentent en réalité lorsque la température diminue (sauf pendant les épisodes caniculaires, mais qui sont rares). Les coefficient Rhô seront alors tous négatifs. Ils seront d’autant plus forts qu’ils seront proches de -1.
Le test de Spearman nous indique que la relation entre température et décès est significative dès 50 ans. L’intensité du lien ne fait ensuite qu’augmenter avec l’âge. Il n’y a aucune relation entre température et mortalité avant 50 ans.
Au-delà de 85 ans, le Rhô de Spearman frise les 0,9 (Figure 13 et Figure 14). Si la température expliquait totalement la mortalité, le coefficient serait de 1. Notre 0,9 ici signifie que des personnes âgées de plus de 85 ans meurent toute l’année, mais les augmentations et baisses de mortalité s’expliquent avec les variations de température quasiment parfaitement. Le peu qui reste peut éventuellement s’expliquer comme du bruit, autrement dit, les aléas de la vie.
Figure 13 : Taux de mortalité en France des plus de 90 ans et température, lissés sur 7 jours
Note de lecture : Le taux de mortalité toutes causes est en notation « scientifique » : 8e-04 signifie 8 décès pour 10 000 habitants. La température est inversée : -10 signifie +10°C.
Figure 14 : Taux de mortalité en France des 85-89 ans et température, lissés sur 7 jours
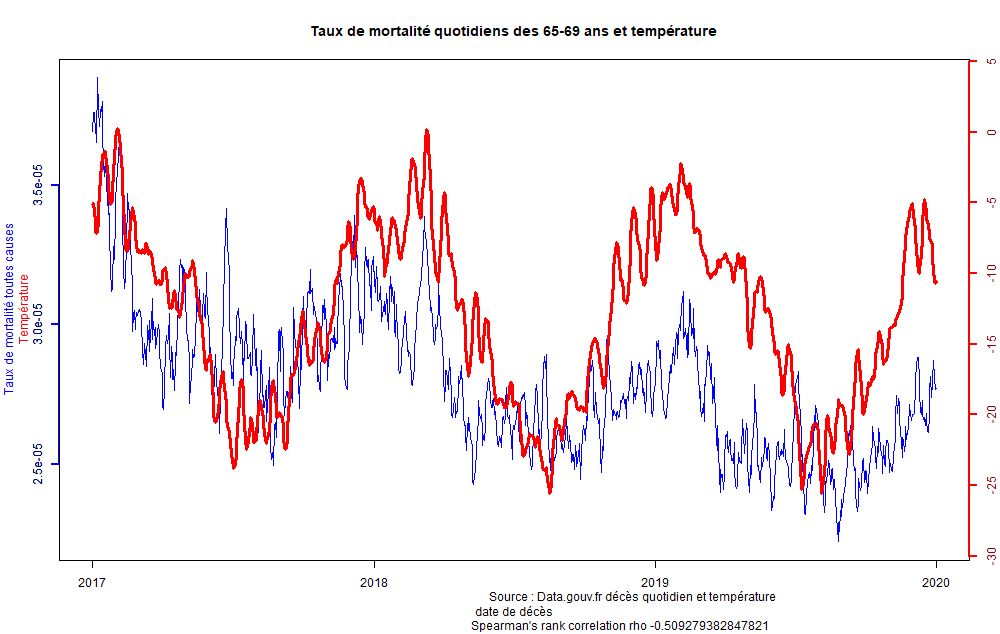
Le Rhô décroît ensuite régulièrement en rajeunissant, tout en restant significatif (Figure 15). Cela signifie que pour les âges plus jeunes, les accidents de la vie pèsent plus par rapport à la température. En effet, plus la population est jeune et moins il y a de décès et donc plus les évènements particuliers vont avoir un impact. Mais aussi visiblement, plus on est jeune et moins on est sensible aux aléas météorologiques dont la température. Entre 65 en 85 ans, le rho est quand même supérieur à 0.5. C’est donc une très forte corrélation, avec surtout moins de décès qu’à plus de 85 ans et moins de sensibilité hivernale.
Figure 15 : Taux de mortalité en France des 65-69 ans et température, lissés sur 7 jours
Le test de Spearman reste significatif entre 50 et 60 ans (Figure 16). Cependant, le Rhô décroît fortement aux âges avant 60 ans. Signe ici d’une vraie période charnière à ces âges sur la santé.
Figure 16 : Taux de mortalité en France des 55-59 ans et température, lissés sur 7 jours
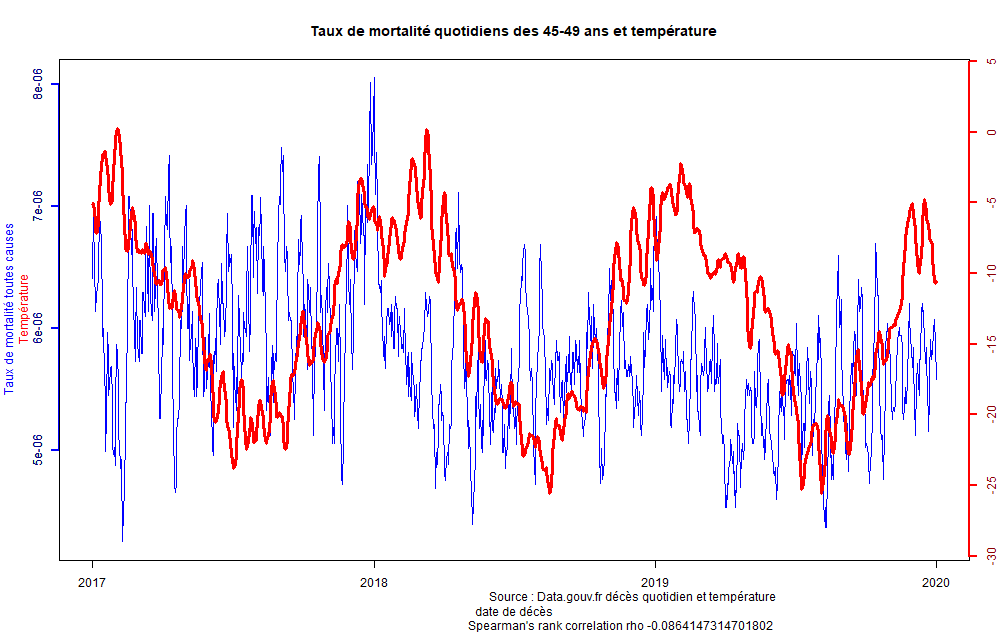
Sur toutes les tranches d’âge avant 50 ans, le test de Spearman n’est plus du tout significatif (Figure 17).
Figure 17 : taux de mortalité en France des 45-49 ans et température, lissés sur 7 jours
Nous savons dorénavant que la température explique bien la mortalité hivernale. Ce résultat est à rapprocher d’autres études, notamment biologiques. Par exemple, il a été observé que la composition cellulaire du sang varie selon la saison. Ces variations peuvent être signe de changements au sein du système immunitaire liés aux conditions météorologiques.13 Nous pouvons tenter de modéliser la mortalité à partir de la température pour les âges pour lesquels cela a du sens et notamment au-dessus de 65 ans. Ici la méthode GAM (modèle additif généralisé)14 est utilisée. Elle consiste à modéliser une statistique à l’aide d’une autre, dans notre cas avec des fonctions polynomiales. L’idée est de savoir si nous pouvons prévoir la mortalité en fonction de la température extérieure.
Il faut avoir en tête qu’à partir du moment que le passage à la modélisation implique de s’écarter de la réalité. Il s’agit d’une construction de l’esprit pour tenter de coller aux relevés et pas d’une explication parfaite du lien. Par exemple, même si le modèle GAM polynomial est puissant, il suppose qu’il n’y a pas d’effet de seuil. Un effet de seuil serait dans notre cas un saut de mortalité. Par exemple, si on imagine que la mortalité n’augmente pas régulièrement, mais que passer sous une certaine température, un grand nombre de personnes meurent d’un coup, cela provoque un effet de seuil. C’est probablement ce que l’on observe dans le graphique des plus de 90 ans. Les effets de seuil entraînent que la fonction de mortalité n’est pas dérivable et ne sera donc pas parfaitement approchée par des polynômes.
De même, le fait que les humains ne meurent qu’une seule fois implique :
• Qu’une forte mortalité après une baisse de température va diminuer le nombre de décès possible
• S’il survient une deuxième baisse de température, il risque d’y avoir moins mécaniquement mois de décès.
Il y a donc des effets d’exclusion qui ne sont pas modélisés ici.
Cela n’empêche pas de travailler, mais permet d’être conscient que la vraie vie ne s’approche pas facilement par des formules mathématiques contrairement à ce qu’essayent de faire croire certaines équipes scientifiques, en économie comme en médecine, qui font du catastrophisme une marque de fabrique et/ou tentent de vendre des produits miracles.
Finalement, pour les plus de 90 ans, on obtient un coefficient de corrélation à 0.7 ce qui fait de ce modèle, rustique et plein de défauts, un très bon modèle de prédiction malgré tout (Figure 18 et Figure 19). Le coefficient de corrélation est maximal à 0,75 pour la tranche d’âge des 85-89 ans, probablement grâce à une moindre importance des effets de seuils et de moisson.
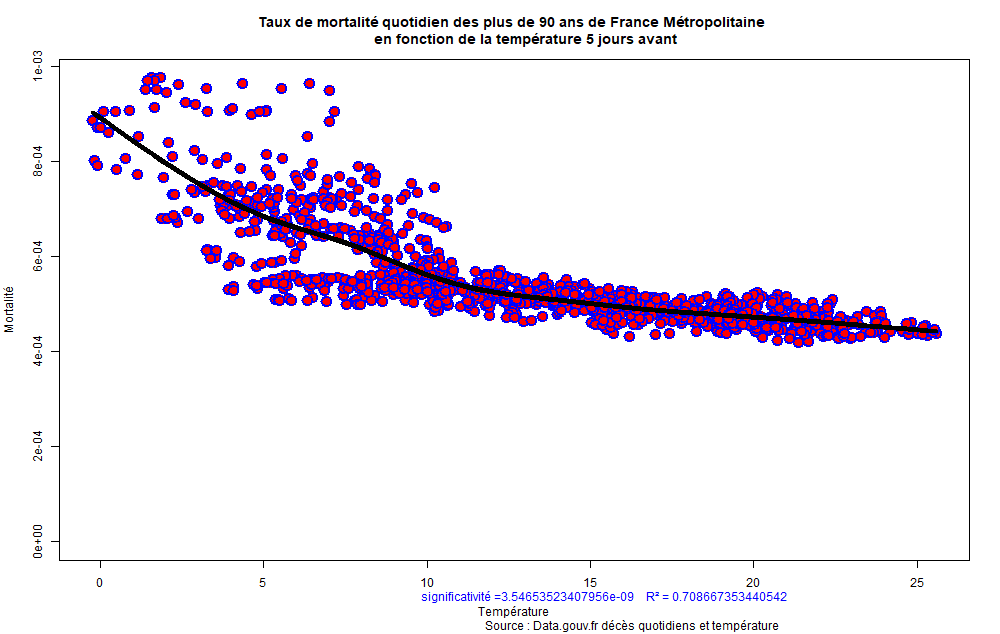
Figure 18 : Taux de mortalité en fonction de la température, données brutes et courbe de GAM
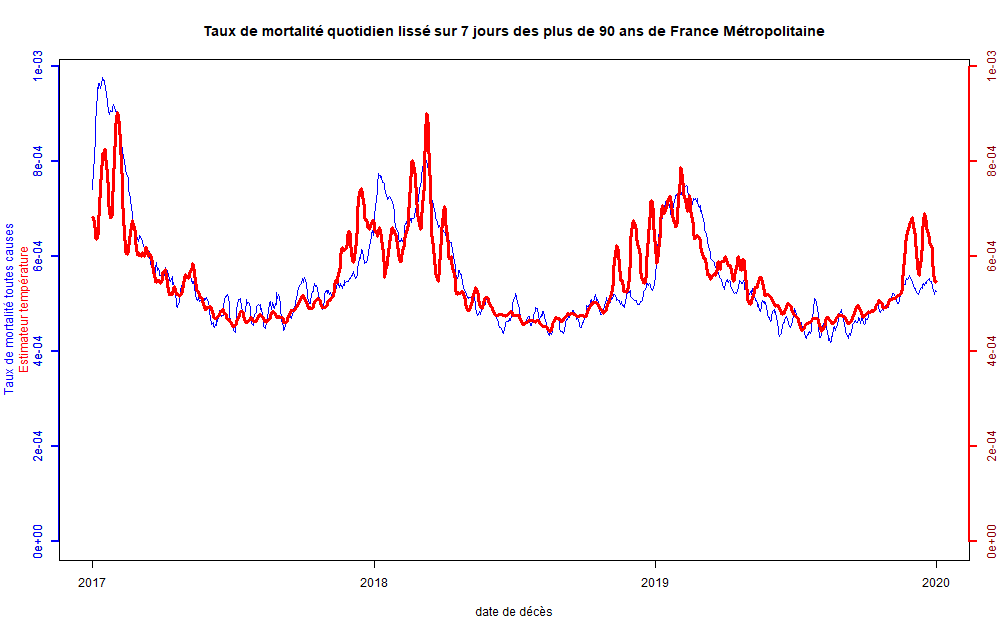
Figure 19 : Taux de mortalité des 90 ans et plus observé et prévu avec la température
On peut constater que la modélisation fonctionne pour tous les départements sur lesquels il y a assez de population pour stabiliser les statistiques. Ci-dessous par exemple les 3 départements les plus peuplés pour la tranche d’âge des 90 ans et plus (Figure 20, Figure 21 et Figure 22).
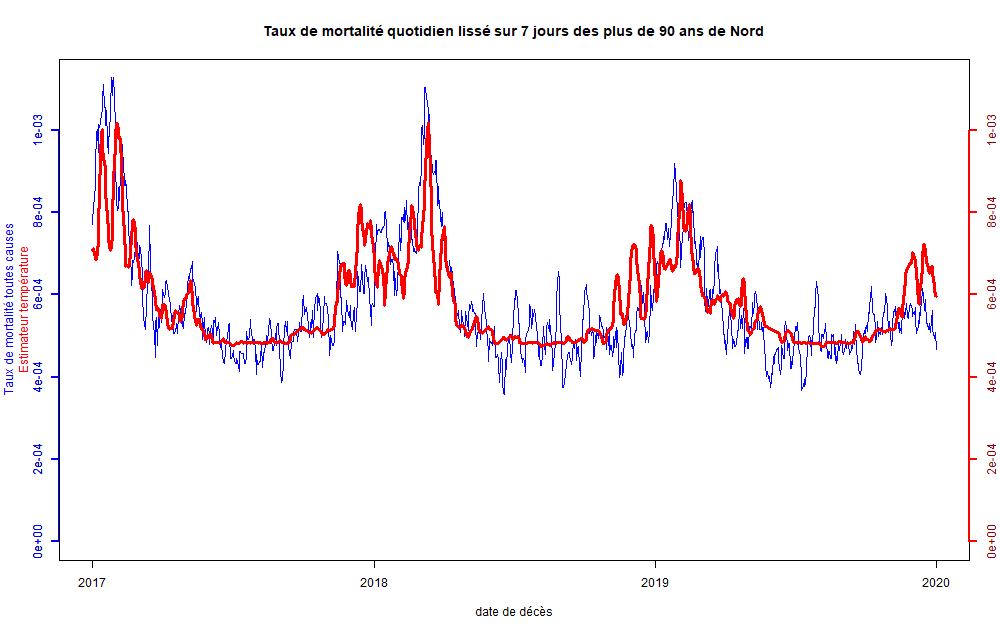
Figure 20 : Taux de mortalité des 90 ans et plus observé et prévu avec la température pour le Nord
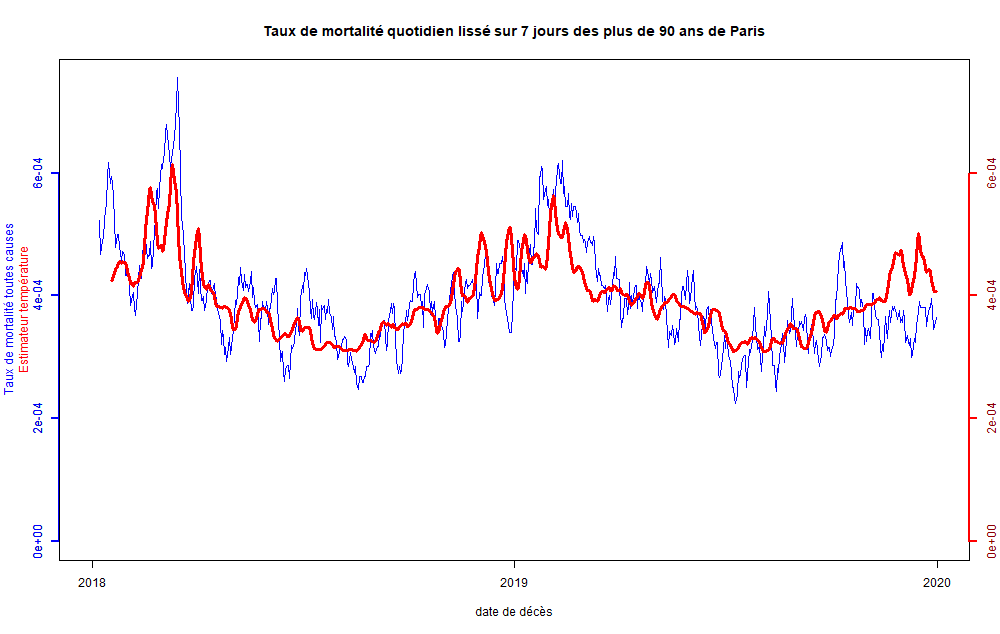
Figure 21 : Taux de mortalité des 90 ans et plus observé et prévu avec la température pour Paris
Figure 22 : Taux de mortalité des 90 ans et plus observé et prévu avec la température pour les Bouches-du-Rhône
Comme nous l’avons vu avec le test de Spearman, la corrélation est d’autant plus forte que l’âge augmente également dans les départements. Il est significatif à partir de 50 ans, mais pas en-dessous. Finalement, le lien fonctionne très bien même à niveau plus fin : les variations de température expliquent les variations de mortalité à partir de 50 ans et la corrélation est d’autant plus forte que l’âge est avancé.
4. En conclusion, les statistiques rejettent l’hypothèse de propagation
et confortent l’hypothèse du changement de conditions extérieures
Nous avons vu dans la première partie que le fait que les hausses et baisses de mortalité soient simultanées partout en même temps invalide l’hypothèse de propagation des maladies hivernales. Si les maladies se propageaient, on verrait des mortalités en décalé.
Dans la deuxième partie, nous avons vu que la mortalité des plus âgés est presque parfaitement corrélée à la température extérieure. Finalement c’est le bon sens qui a raison devant la théorie même si elle s’appuie sur des jolies formules. Les gens qui n’ont pas perdu pied avec la réalité savent encore que :
- L’hiver, il fait froid et on tombe malade.
- Quand on est vieux et malade, on risque plus de mourir que quand on est jeune et en bonne santé.
Ainsi, la mortalité hivernale n’est pas due à l’arrivée d’un virus particulier, mais bien à la dégradation de l’état de santé liée au changement météorologique. Cela ne signifie pas que les contaminations n’existent pas du tout, mais elles sont au mieux des épiphénomènes dans la masse qu’est l’augmentation de la mortalité hivernale. Il est donc complètement vain de faire de l’isolement des humains l’hiver une priorité de santé publique, cela ne va rien changer ni à l’augmentation de la mortalité, ni à celle des hospitalisations.
L’autre résultat, c’est que la politique vaccinale qui vise à lutter contre chaque virus un par un, n’aura mécaniquement pas le moindre impact visible sur la mortalité ou la maladie. Les virus ne sont pas les causes uniques des hausses de mortalité. Ils sont une résultante observable d’une dégradation de la santé liée aux conditions extérieures. Ces conditions rendent malades les gens avec de multiples pathologies. Vouloir attribuer ces hausses de décès à des virus particuliers, comme les grippes, arrange énormément les producteurs de vaccins antigrippaux, et les gouvernements qui les achètent, pour faire croire qu’ils s’occupent de votre santé. Au passage, cela permet de détruire l’hôpital public, tout en continuant de dépenser toujours plus d’argent, lui aussi public, mais pour le diriger vers les bonnes poches.
Maintenant que nous avons vu ce lien entre 2017 et 2020, nous allons voir ce qu’il se passe si on prolonge notre modèle en 2020 et 2021. Nous allons étudier les écarts entre les décès prévu par la température et ce que nous avons vécu.
Pierre Lecot, de la chaîne « Décoder l’éco »
Sources :
⚠ Les points de vue exprimés dans l’article ne sont pas nécessairement partagés par les (autres) auteurs et contributeurs du site Nouveau Monde.
- [1] – https://ec.europa.eu/eurostat/documents/3859598/5926869/KS-RA-13-028-EN.PDF/e713fa79-1add-44e8-b23d-5e8fa09b3f8f[↩]
- [2] – https://www.who.int/data/gho/indicator-metadata-registry/imr-details/78[↩]
- [3] – https://www.nrscotland.gov.uk/files/statistics/age-standardised-death-rates-esp/age-standard-death-rates-background.pdf[↩]
- [4] – https://www.mondialisation.ca/la-mortalite-en-europe-comprendre-les-donnees-de-mortalite-europeenne-pour-prendre-les-bonnes-decisions/5657446[↩]
- [5] – https://www.youtube.com/watch?v=ufivMhlZ6Us[↩]
- [6] – https://fr.wikipedia.org/wiki/Mod%C3%A8les_compartimentaux_en_%C3%A9pid%C3%A9miologie[↩]
- [7] – https://www.addactis.com/fr/modeles-epidemiologiques-problematiques-calibrage-donnees-covid-19/[↩]
- [8] – https://www.senat.fr/fileadmin/Fichiers/Images/opecst/quatre_pages/OPECST_modelisation_covid_19.pdf[↩]
- [9] – https://www.assemblee-nationale.fr/dyn/15/comptes-rendus/ots/l15ots1920067_compte-rendu.pdf[↩]
- [10] – https://www.insee.fr/fr/statistiques/4771989?sommaire=4772633[↩]
- [11] – https://public.opendatasoft.com/explore/dataset/donnees-synop-essentielles-omm/table/?sort=date[↩]
- [12] – https://fr.wikipedia.org/wiki/Corr%C3%A9lation_de_Spearman[↩]
- [13] – https://www.nature.com/articles/ncomms8000[↩]
- [14] – https://fr.wikipedia.org/wiki/Mod%C3%A8le_additif_g%C3%A9n%C3%A9ralis%C3%A9[↩]