11/05/2023 (2022-09-23)
[Source : science-climat-energie.be]
[NDLR Regroupement de plusieurs articles écrits sur le sujet par le professeur Georges Geuskens.]
Par Georges Geuskens, Professeur émérite de l’Université Libre de Bruxelles (ULB)
Le CO2 dans les basses couches atmosphériques (partie 1)
Certains climatologues estiment, sur la base de modèles informatiques, que l’augmentation de la teneur en CO2 dans l’atmosphère pourrait avoir une influence sur le climat. Avant d’aborder ce problème il est important d’analyser le comportement de ce gaz dans les basses couches atmosphériques.
A cette fin envisageons une boîte opaque contenant, à l’abri de tout rayonnement extérieur, une certaine quantité d’air sec à 15°C et à la pression d’une atmosphère. Dans cette boîte 78 % des molécules sont des molécules d’azote N2 et 21 % sont des molécules d’oxygène O2. Le troisième constituant par ordre d’abondance est l’argon Ar (environ 1 % des molécules). Les molécules de CO2 n’interviennent que pour environ 0,04 %. Toutes ces molécules n’ont pratiquement pas d’interaction entre elles, si ce n’est qu’étant en constante agitation elles entrent en collisions les unes avec les autres lors de chocs dont la plupart sont élastiques (avec conservation de l’énergie cinétique). La théorie cinétique des gaz permet de calculer qu’à la température de 15°C les molécules de l’air sont animées de vitesses de l’ordre de 500 m par seconde (voir fig. 1, courbe à 300 K) et qu’à cette température et à la pression d’une atmosphère chacune subit plusieurs milliards de collisions par seconde. De plus, ces molécules présentent une large distribution de vitesses qui est fonction de la température en accord avec la loi de Maxwell-Boltzmann (Fig. 1).

Les molécules de l’air ne sont pas seulement animées de mouvements de translation. Si elles disposent de l’énergie suffisante elles peuvent aussi entrer en vibration avec variation rapide et périodique des longueurs ou des angles de leurs liaisons interatomiques. Contrairement aux mouvements de translation dont l’énergie peut varier d’une manière continue seuls certains niveaux énergétiques de vibration sont permis. La mécanique quantique nous apprend, en effet, que l’énergie de vibration ne peut varier de manière continue. A chaque fréquence de vibration permise est associée une énergie qui peut être déterminée expérimentalement par spectroscopie d’absorption dans le domaine infrarouge ou Raman. Les molécules biatomiques N2 et O2 sont très rigides et ne vibrent pratiquement pas à 15°C. Par contre, les molécules triatomiques de CO2, linéaires à l’état fondamental O=C=O, peuvent se déformer facilement et devenir anguleuses en vibrant. L’énergie de cet état de vibration peut être calculée à partir de la bande d’absorption détectée à 15 µm dans le spectre infrarouge du CO2 grâce à la relation Ev = hc /λ (où h est la constante de Planck, c la vitesse de la lumière et la longueur d’onde du rayonnement absorbé, dans ce cas 15 µm). Cette valeur n’est que de 30 % supérieure à l’énergie cinétique moyenne des molécules environnantes N2 et O2 qui, d’après la théorie cinétique des gaz, vaut Ec = 5/2 k T (où k est la constante de Boltzmann et T la température en Kelvin). Or, beaucoup de molécules ont une vitesse et donc une énergie cinétique supérieure à la moyenne comme l’indique la fig. 1 (la vitesse moyenne est très proche du maximum de la courbe de distribution des vitesses).
En l’absence d’une source extérieure de rayonnement l’énergie nécessaire pour exciter la vibration de CO2 ne peut provenir que de l’énergie d’agitation thermique du milieu ambiant. La quantification de l’énergie n’intervenant pas au niveau des mouvements de translation les énergies cinétiques de translation Ec = mv2/2 présentent une large distribution continue semblable à celle illustrée sur la fig. 1. La fonction mathématique correspondant à ces courbes permet de calculer qu’à 15°C plus de 40 % des molécules N2 et O2 ont suffisamment d’énergie cinétique pour amener les molécules de CO2 à leur plus bas niveau de vibration lors d’une collision inélastique (sans conservation de l’énergie cinétique). Dans ces conditions il y a conversion d’une fraction ∆ de l’énergie cinétique de translation des molécules N2 ou O2 en énergie de vibration du CO2 :
∆Ec (translation) de N2 + CO2 ↔ ∆Ev (vibration) de CO2 + N2 (1)
Ce ne sont évidemment pas toujours les mêmes molécules de CO2 qui sont en état de vibration car cette conversion est réversible et les molécules se désactivent endéans quelques microsecondes pour retourner à l’état fondamental lors de nouveaux chocs avec les molécules environnantes qui, de ce fait, acquièrent temporairement un surcroît d’énergie cinétique de translation.
Il existe donc un équilibre dynamique résultant des très nombreuses collisions. Il ne dépend que de la température et de la pression (par le biais de la distribution des énergies et du nombre de chocs entre molécules). Quoique ce ne soient pas toujours les mêmes molécules de CO2 qui vibrent la proportion de molécules en état de vibration reste constante à une température et une pression déterminées (environ 40 % à 15°C et à la pression d’une atmosphère).
Les molécules de CO2 amenées à l’état de vibration pourraient-elles se désactiver par réémission du rayonnement de 15 µm correspondant à l’excédent d’énergie de ce niveau par rapport à l’état fondamental ? Un tel phénomène de désactivation radiative est bien connu entre niveaux d’énergie électronique et est appelé fluorescence mais il n’a été observé entre niveaux d’énergie de vibration qu’à très haute altitude à des pressions extrêmement faibles (voir paragraphe 2c ici ). La raison en est qu’en solution ou en phase gazeuse à des pressions voisines d’une atmosphère la désactivation radiative ne peut entrer en compétition avec la désactivation par collisions que pour des états excités de très courte durée de vie (10-9 à 10-7 s). Ces derniers peuvent alors émettre un rayonnement avant qu’une collision inélastique se produise. Ce n’est pas le cas des états de vibration dont la durée de vie est de l’ordre des millisecondes. L’équilibre (1) ne sera donc pas modifié si certaines molécules de CO2, en plus des collisions dues à l’agitation thermique, étaient excitées par absorption d’un rayonnement de longueur d’onde appropriée λ (15 µm en l’occurrence) car cet apport d’énergie serait rapidement converti en un surcroît d’énergie de translation des molécules environnantes. Le fait qu’à 15°C et à la pression d’une atmosphère les molécules de CO2 à l’état de vibration ne peuvent se désactiver par réémission d’un rayonnement est une conclusion essentielle pour comprendre l’influence que ce gaz pourrait avoir sur le climat.
Le CO2 dans les basses couches atmosphériques (partie 2)
La présence de CO2 dans les basses couches atmosphériques peut-elle avoir une influence sur le climat en modifiant le bilan énergétique global de la Terre ? Le bilan énergétique doit tenir compte du fait que pour maintenir une température constante la Terre doit dissiper l’énergie reçue du Soleil et que différents mécanismes de dissipation sont possibles. Le modèle le plus complet est celui proposé par la NASA (fig. 1).
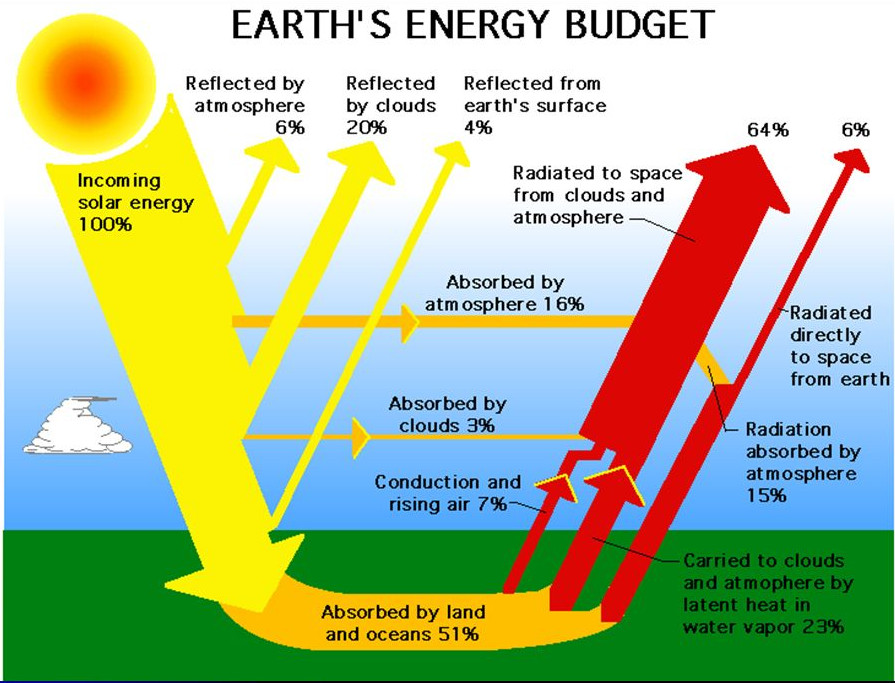
D’après ce bilan 30 % de l’énergie reçue par la Terre au sommet de l’atmosphère seraient réfléchis par les nuages, l’atmosphère et la surface terrestre : c’est l’albédo de la Terre. L’atmosphère et les nuages absorberaient en plus 19 % du rayonnement solaire transmis et finalement 51 % seulement seraient absorbés par les continents et les océans. Cette énergie serait dissipée ensuite par trois mécanismes distincts : évaporation de l’eau des océans (23 %), convection de l’air (7 %) et rayonnement thermique (21 %). Remarquons sur la fig. 1 qu’une petite fraction seulement de l’énergie détectée au sommet de l’atmosphère sous forme de rayonnement provient directement de la surface terrestre (fine flèche rouge à droite). Finalement toute l’énergie dissipée par la surface terrestre (quel que soit le mécanisme) ou absorbée directement par l’atmosphère et les nuages est convertie en rayonnement dans les couches supérieures de l’atmosphère (large flèche rouge) car c’est le seul mécanisme d’évacuation de cette énergie hors de l’atmosphère terrestre. Le rayonnement détecté par satellite à haute altitude (70 % de l’énergie reçue par la Terre au sommet de l’atmosphère) provient donc essentiellement des couches supérieures de l’atmosphère à des températures beaucoup plus froides que la surface terrestre.
Si on considère la Terre comme un corps noir à 15°C l’équation de Planck (fig. 1 ici ) permet de calculer que 95 % du spectre d’émission sera compris entre 5 et 40 µm et la loi de Wien prévoit que le rayonnement émis devrait présenter un maximum d’intensité à 10 µm. D’après le bilan proposé par la NASA 15 % du rayonnement thermique émis par la Terre sont absorbés par divers constituants atmosphériques. La fig. 2 montre qu’il s’agit principalement de la vapeur d’eau mais aussi du CO2.
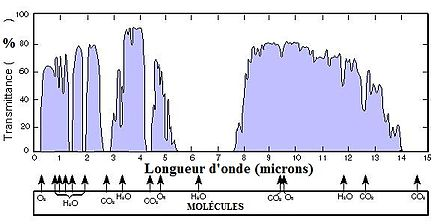
Des zones de transparence atmosphérique apparaissent (en bleu sur la figure), notamment entre 8 à 13 µm. En intégrant l’équation de Planck dans cet intervalle de longueurs d’onde on trouve que 30 % du rayonnement thermique de la Terre est émis dans cette zone de transparence atmosphérique soit env. 6 % de l’énergie totale reçue du Soleil au sommet de l’atmosphère (30 % de 21 %). Ce résultat est en accord avec le bilan de la NASA (fig. 1) qui fait effectivement état de 6 % d’énergie rayonnée directement vers l’atmosphère.
Le CO2 présente une bande d’absorption dans le domaine du rayonnement thermique de la Terre. Elle est présentée sur la fig. 3 pour une teneur en CO2 de 357 ppm (0,0357 %) en présence de 2,6 % en vapeur d’eau, conditions correspondant à la composition atmosphérique en 1993 (date d’enregistrement du spectre).
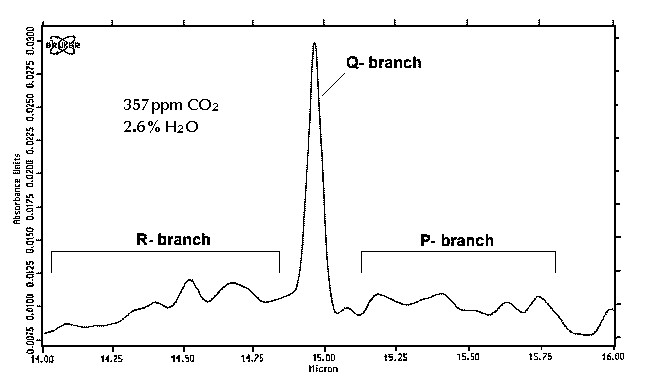
Cette bande d’absorption centrée à 15 µm (branche Q) permet l’excitation de la molécule à un état de vibration impliquant sa déformation angulaire. Les branches P et R sont dues à l’existence de sous-niveaux de rotation pour chaque niveau de vibration (fondamental et excité). En intégrant l’équation de Planck cette fois dans le domaine de 14 à 16 µm, domaine d’absorption du CO2, on calcule que 9,3 % du rayonnement thermique de la Terre est émis dans cet intervalle de longueurs d’onde. En fin de compte le CO2 , quel que soit son coefficient d’absorption, ne pourrait absorber au maximum que 9,3 % du rayonnement thermique de la Terre (représentant 21 % de l’énergie totale reçue du Soleil) soit un peu moins de 2 % de l’énergie totale reçue du Soleil au sommet de l’atmosphère.
Les molécules de CO2 excitées à l’état de vibration par absorption d’une fraction du rayonnement thermique de la Terre ont une durée de vie limitée. Elles se désactivent endéans quelques microsecondes par collisions avec les molécules environnantes (voir ici ), principalement N2 et O2. Dans ces conditions il y a conversion d’une fraction ∆ de l’énergie de vibration du CO2 en énergie cinétique de translation des molécules N2 (ou O2) :
∆Ev (vibration) de CO2 + N2 → ∆Ec (translation) de N2 + CO2
Bien que l’absorption du rayonnement thermique de la Terre entre 14 et 16 µm soit sélective par les molécules de CO2 (fig. 2 et 3) cet excédent d’énergie se répartit sur l’ensemble des molécules environnantes suite aux multiples collisions. Au total 2 % de l’énergie reçue du Soleil au sommet de l’atmosphère terrestre seront convertis en mouvements de convection au détriment de l’intensité du rayonnement thermique.
En conclusion la présence de CO2 dans l’atmosphère ne modifie pas le bilan énergétique global de la Terre mais seulement l’importance relative des différents mécanismes de dissipation de l’énergie reçue du Soleil. Ceci ne peut avoir aucune influence sur la température globale moyenne de la surface terrestre.
Forçage radiatif, sensibilité climatique et rétroactions positives
Le forçage radiatif (radiative forcing) peut être défini comme la différence entre l’énergie radiative reçue du Soleil et l’énergie radiative émise vers l’espace par la Terre. Ce concept a été introduit par les partisans d’un réchauffement climatique d’origine anthropique pour donner une base quantitative à la théorie de l’effet de serre défini comme :
« un phénomène radiatif causé par des gaz tels la vapeur d’eau ou le CO2 qui absorbent une fraction du rayonnement infrarouge émis par la Terre et le réémettent ensuite dans toutes les directions et notamment vers la surface terrestre dont la température serait, de ce fait, plus élevée qu’en l’absence de gaz absorbant l’infrarouge ».
Le forçage radiatif ∆F dû au CO2 correspond donc à la fraction du rayonnement thermique de la Terre qui serait absorbée par ce gaz puis réémise vers la Terre. Il en résulterait une perturbation du bilan énergétique de la Terre dont la température devrait, selon les partisans d’un réchauffement climatique d’origine anthropique, augmenter pour dissiper plus d’énergie par rayonnement thermique afin d’atteindre un nouvel équilibre.
La version la plus récente de la formule semi-empirique utilisée par le GIEC pour lier le forçage radiatif à la teneur en CO2 dans l’atmosphère provient d’un article de G. Myrhe et coll. paru en 1998 dans Geophysical Research Letters (vol 25, p. 2715) et intitulé « New estimates of radiative forcing due to well mixed greenhouse gases » :
∆F (W m-2) = 5,35 ln C/C0 (1)
Dans cette formule C est la concentration du CO2 en ppmv (parties par million en volume) à un moment donné et C0 la concentration de référence, par exemple avant le début de l’ère industrielle (278 ppmv). Elle est obtenue en introduisant des teneurs en CO2 extrapolées jusqu’à 1000 ppmv dans plusieurs modèles climatiques globaux sans tenir compte d’un effet de saturation de l’absorption qui interviendra nécessairement avec l’augmentation de la teneur en CO2. Les résultats sont rassemblés sur la fig. 1 extraite de l’article cité. La relation (1) décrit l’allure de ces courbes.

(d’après Myrhe 1998)
En 2005 le forçage radiatif depuis le début de l’ère industrielle était estimé par le GIEC à 1,7 W m-2 mais actuellement avec une teneur en CO2 dans l’atmosphère proche de 400 ppmv la valeur déduite de la formule (1) serait de 2 W m-2.
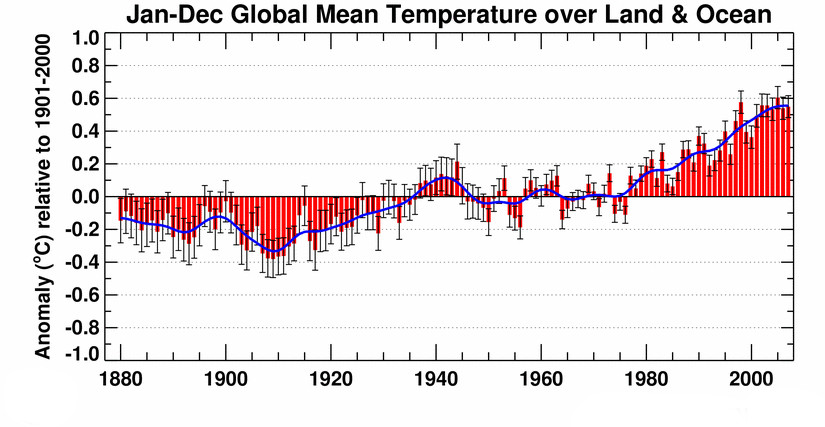
Il faut remarquer que la publication de Myrhe date de 1998 et correspond à une période allant approximativement de 1980 à 2000 pendant laquelle les partisans d’un réchauffement climatique d’origine anthropique ont voulu établir une corrélation entre l’augmentation de température moyenne globale (fig. 2) et l’augmentation de la teneur en CO2 dans l’atmosphère. Cependant depuis près de 20 ans la température ne varie pratiquement plus (fig. 3), bien que la teneur en CO2 n’ait cessé d’augmenter d’environ 2 ppmv par an.
Le problème est d’établir un lien entre le forçage radiatif estimé d’après la formule (1) et l’augmentation de température qui en résulterait selon la théorie de l’effet de serre. A cet effet les climatologues se basent toujours sur la formule de Stefan Boltzmann qui lie la puissance rayonnée par unité de surface F à la température T (en K) à la puissance 4 :
F (W m-2) = σ T4 (σ = constante de Stefan = 5,67 x 10-8 W m-2 K-4)
Si le CO2 donne lieu à un forçage radiatif estimé à 2 W m-2 ils considèrent que la température de la Terre devrait nécessairement augmenter pour dissiper sous forme de rayonnement thermique ce surcroît d’énergie reçue. Or, il est bien établi que deux autres mécanismes contribuent également, et de manière prépondérante, à la dissipation de l’énergie par la Terre : la convection de l’air et l’évaporation de l’eau des océans. La formule de Stefan Boltzmann sous la forme mentionnée ci-dessus n’en tient pas compte.
Certains climatologues écrivent néanmoins sur la base de la formule de Stefan Boltzmann :
T4 (actuel) / T4 (préindustriel) = F + ∆F / F (2)
Si la puissance F rayonnée au sommet de l’atmosphère était de 240 W m-2 au début de l’ère industrielle et si le forçage radiatif ∆F est aujourd’hui de 2 W m-2 le rapport des F vaudrait 242/240 = 1,008 et le rapport des T = 1,002. On en déduit que si la température était 288 K au début de l’ère industrielle elle deviendrait 288,6 K aujourd’hui soit une augmentation de température de 0,6 °C. Une méthode différente utilisée par d’autres climatologues est basée cette fois sur la dérivée de la formule de Stefan Boltzmann qui pourrait s’écrire :
dF/dT = 4 σ T3 d’où ∆F = 4 σ T3 ∆T (3)
Avec un forçage radiatif de 2 W m-2 et si la température était 288 K au début de l’ère industrielle on trouve cette fois ∆T = 0,37 °C.
En réalité la fig. 2 montre que l’augmentation globale de température enregistrée depuis 1880 ne suit ni l’une ni l’autre des relations (2) et (3). Elle est globalement de 0,7 °C mais passe par un minimum en 1910 suivi d’un petit maximum en 1940, d’un palier de 1950 à 1980 et d’une remontée à partir de 1980 pour se stabiliser depuis l’an 2000 approximativement.
La sensibilité climatique est définie comme l’augmentation de température qui résulterait d’un doublement de la concentration en CO2 pour atteindre 800 ppmv (en 2200 au taux de croissance actuel). La valeur trouvée serait comprise entre 0,7 et 1,4 °C sur la base des relations (2) ou (3) donc de l’ordre de 1°C par rapport à aujourd’hui. Ce n’est pas très important mais des rétroactions positives peuvent amplifier cet effet. On peut faire intervenir, par exemple, la vapeur d’eau, autre gaz à « effet de serre », dont la concentration augmenterait suite à l’élévation de température ou la fonte de la banquise et la diminution des surfaces enneigées qui auraient pour effet de diminuer l’albédo de la Terre et donc la fraction d’énergie solaire réfléchie. Pour une revue d’une douzaine de possibilités de rétroactions positives voir ici.
Pour calculer la sensibilité climatique une formule censée tenir compte de différentes rétroactions est proposée ici :
∆T = 0,8 ∆F (4)
Avec ∆F = 3,7 W m-2 calculé par la formule (1) pour un doublement de la concentration en CO2 la formule (4) conduit à une augmentation de température de 3 °C, valeur adoptée par la National Academy of Sciences (Washington) en 1979 avec une marge d’erreur de 1,5 °C selon l’importance relative attribuée aux diverses rétroactions dans différents modèles climatiques globaux.
Il est évident que l’intervention de divers types de rétroaction permet l’introduction de nombreux paramètres dans différents modèles climatiques globaux. Dès lors tous les ajustements sont possibles entre la réalité climatique et les modèles théoriques comme l’illustre la fig. 3.

(moyenne des mesures par ballons-sondes en vert , par satellites en bleu)
et prédictions selon différents modèles climatiques
(ligne rouge = moyenne de 102 modèles)
Du bon usage de la formule de Stefan-Boltzmann
La formule de Stefan-Boltzmann est l’outil de travail des climatologues qui veulent prédire des variations de température à partir des flux énergétiques intervenant dans le bilan énergétique de la Terre ( voir ici ). Sous la forme utilisée, elle lie le flux unidirectionnel F rayonné (vers la Terre ou vers l’espace) à la température T (en K) à la puissance 4 (σ = constante de Stefan = 5,67 x 10-8 W m-2 K-4) :
F (W m-2) = σ T4 (1)
Rappel théorique
La formule de Stefan-Boltzmann est dérivée de la théorie du « corps noir » élaborée par plusieurs physiciens dans la seconde moitié du 19ème siècle pour établir un lien entre le flux de rayonnement émis par tout solide à une température supérieure au zéro absolu et la température de ce solide. La meilleure représentation qu’on puisse se faire du modèle sur lequel est basée cette théorie est celle d’un four sous vide et à l’équilibre thermique dont la paroi interne opaque absorbe, sans aucune réflexion ni transmission, tout rayonnement électromagnétique quelle que soit sa longueur d’onde. A l’équilibre thermique elle doit également réémettre tout rayonnement absorbé. Ce four parfaitement isolé devrait cependant être percé d’un minuscule orifice permettant d’analyser le rayonnement concentré à l’intérieur. Aucune interprétation quantitative du spectre observé ne fut possible dans le cadre de la théorie électromagnétique classique et c’est finalement Planck qui proposa en 1900 une équation introduisant l’idée, révolutionnaire pour l’époque, qu’à chaque longueur d’onde le rayonnement ne peut être émis que sous forme de « quanta » (c’est-à-dire de petits paquets) dont l’énergie est hν = hc/λ (où ν et λ sont respectivement la fréquence et la longueur d’onde du rayonnement, c la vitesse de la lumière et h une nouvelle constante de la nature appelée désormais constante de Planck). Ce rayonnement qualifié de « thermique » est dû à l’oscillation de dipôles électriques formés par le noyau et le nuage électronique des atomes qui, en accord avec les lois de l’électromagnétisme, émettent un rayonnement de fréquence égale à la fréquence d’oscillation.
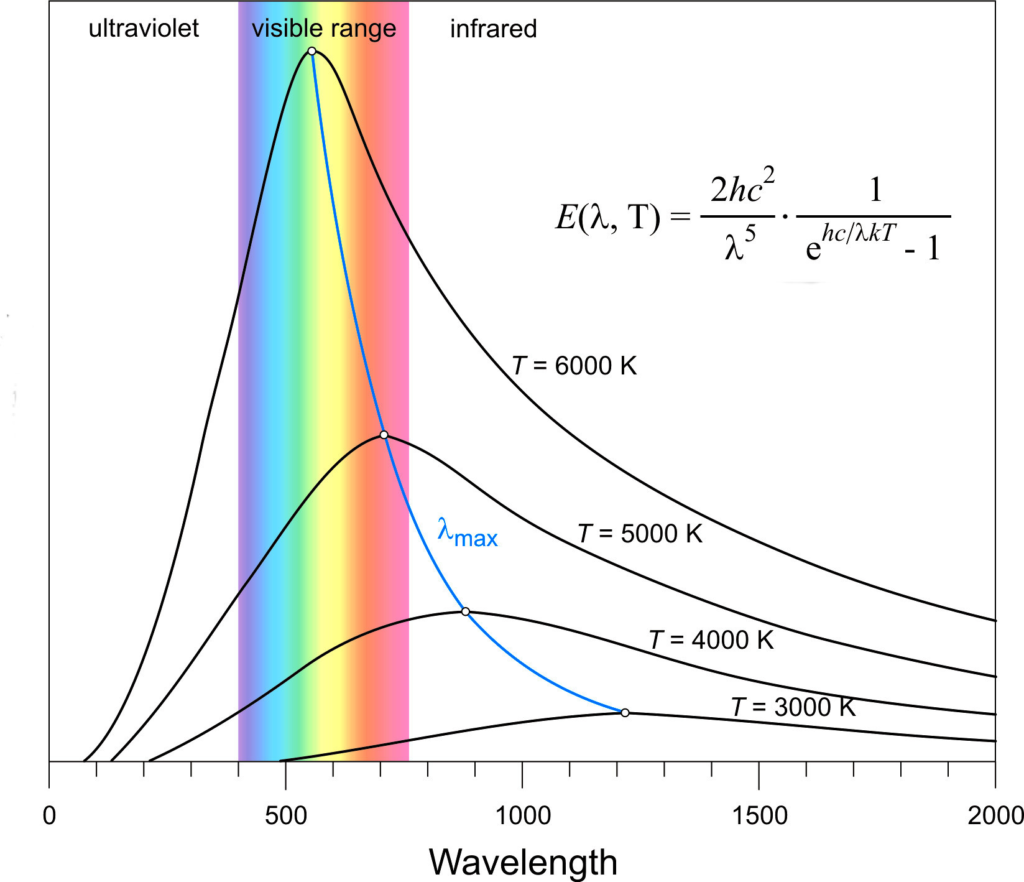
L’équation de Planck (mentionnée sur la fig. 1) permet de calculer à différentes températures l’émittance monochromatique hémisphérique E(λ, T) en W m-2 c’est-à-dire le flux par unité de surface émis à chaque longueur d’onde dans toutes les directions à partir d’une surface plane. Les courbes obtenues sont présentées sur la fig. 1. Elles sont indépendantes de la nature du corps.
L’intégration de l’équation de Planck sur tout le domaine de longueurs d’onde conduit à la formule de Stefan-Boltzmann qui lie l’émittance hémisphérique totale E(T) (en W m-2) à la température T (en K) à la puissance 4 (σ = constante de Stefan) :
E (T)(W m-2) = σ T4 (2)
La relation (2) fournit une mesure de l’aire sous les courbes de la fig. 1. Il faut remarquer que l’émittance énergétique hémisphérique E(T) intervenant dans la relation (2) est physiquement différente du flux unidirectionnel F de la relation (1). Cette dernière, couramment utilisée en climatologie, peut être considérée comme une approximation à usage pratique. La fig. 1 montre aussi que le maximum de la courbe d’émission se déplace avec la température selon la loi de Wien :
λmax = C / T (C = 2,9 10-3 m K).
Limitations pratiques
L’application de l’équation de Planck et de la formule de Stefan-Boltzmann à des substances réelles bien différentes du modèle théorique implique certaines limitations.
1° En présence d’un autre corps à une température supérieure au zéro absolu, émettant donc aussi un rayonnement thermique, l’échange énergétique radiatif obéira à la relation :
F (W m-2) = σ (Tc4 – Tf4)
Dans cette formule Tc et Tf sont respectivement les températures des corps chaud et froid impliqués dans l’échange énergétique (le symbole F correspond toujours à un flux unidirectionnel comme il est d’usage en climatologie). Le rayonnement émis par un corps froid ne peut donc pas être absorbé par un corps chaud. A titre d’exemple, on remarque sur la fig. 1 que toutes les longueurs d’onde émises par un corps à 3000 K sont déjà émises par un corps à 4000 K. Elles ne pourront donc être absorbées pour exciter l’oscillation de nouveaux dipôles dans ce corps plus chaud.
2° En toute rigueur l’équation de Planck et la formule de Stefan-Boltzmann ne peuvent être utilisées que si le rayonnement thermique est le seul mécanisme d’échange énergétique. Elle ne peut donc s’appliquer à la Terre où la convection de l’air et l’évaporation de l’eau des océans contribuent de manière prépondérante au bilan énergétique ( voir la fig. 1 ici ). Si les satellites détectent au sommet de l’atmosphère l’émission sous forme de rayonnement de 240 W m-2 on ne peut en déduire, par application de la formule (1), que la surface terrestre devrait être à la température de 255 K (-18°C). De même, le fait que la température « globale moyenne » de la Terre soit 288 K (15°C) ne permet pas d’en déduire que le flux radiatif émis par la Terre serait de 390 W m-2
3° Dans la pratique, la surface d’un corps réel ne se comporte pas comme celle d’un corps noir notamment car une partie du flux incident est réfléchie. On définit alors l’émissivité ε d’un corps quelconque comme le rapport entre le flux d’énergie radiative émis par ce corps et le flux d’énergie radiative qui serait émis par un corps noir à la même température. Pour un corps noir ε = 1 et pour un corps réel ε < 1. On qualifie ces corps de « gris » si l’équilibre thermique est néanmoins maintenu à toutes les longueurs d’onde ce qui implique que le flux émis reste égal au flux absorbé. L’absorptivité α d’un corps « gris » (définie de manière analogue à son émissivité) doit donc toujours être égale à son émissivité : α = ε (loi du rayonnement de Kirchhoff). Si α ≠ ε le corps n’est ni gris, ni noir et est hors d’équilibre thermique. Dans le cas d’un corps « gris » la formule de Stefan-Boltzmann devrait s’écrire :
F (W m-2) = ε σ T4 (3)
A une même température le flux radiatif émis par un corps gris sera moindre que celui émis par un corps noir. Les courbes de Planck seront semblables à celles de la fig. 1 mais les intensités émises seront plus faibles.
4° D’une manière générale, lorsque la surface d’un corps est soumise à un rayonnement incident, une fraction ρ (réflectivité) de l’énergie incidente est réfléchie, une fraction α (absorptivité) est absorbée et une fraction τ (transmissivité) est transmise (fig. 2). L’importance de ces différentes fractions dépend de la longueur d’onde et de la température mais la conservation de l’énergie implique toujours que : ρ + α + τ = 1. Dans le cas d’un corps noir ou gris τ = 0 d’où α = 1 – ρ. De plus, α = ε d’après la loi du rayonnement de Kirchhoff. Dans l’un et l’autre cas la formule de Stefan -Boltzmann peut être utilisée sous la forme (1) ou (3) mais elle n’est pas valable si τ ≠ 0.
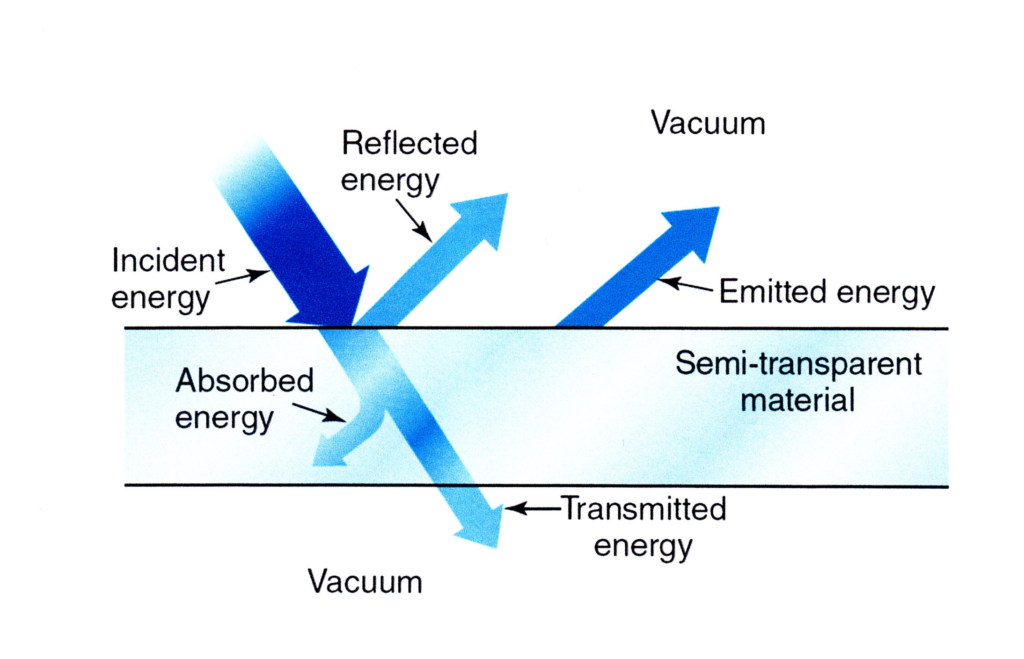
Dans le bilan énergétique de la Terre proposé par la NASA (voir la fig.1 ici) 4 % du flux radiatif d’origine solaire sont réfléchis par la surface terrestre (ρ = 0,04). L’absorptivité moyenne de la Terre serait donc α = 0,96. La Terre pourrait être considérée comme un corps gris si ce n’est que 71 % de sa surface sont occupés par des mers ou des océans. Or, l’eau est pratiquement transparente dans le domaine le plus intense du rayonnement solaire (400 nm à 1 µm) où son coefficient d’absorption est très faible (fig. 3). Comme τ ≠ 0 dans ce domaine de longueurs d’onde elle ne peut être considérée comme un corps gris et la formule de Stefan-Boltzmann n’est pas applicable.

Néanmoins, pour estimer la température de surface des océans, des mesures du rayonnement émis ont été faites par satellite dans la fenêtre de transparence atmosphérique de 8 à 13 µm (voir la fig. 2 ici ) où le coefficient d’absorption de l’eau est beaucoup plus élevé (fig. 3). Dans cet intervalle de longueurs d’onde la pénétration du rayonnement solaire est limitée à quelques µm de la surface et τ = 0. La formule de Stefan-Boltzmann a alors été utilisée pour déterminer la température de surface de la mer et des océans dans différentes régions du globe. Il ne faut cependant pas oublier (voir rappel théorique) que la formule de Stefan-Boltzmann est obtenue par intégration de l’équation de Planck sur tout le domaine de longueurs d’onde rayonné et que relation en T à la puissance 4 n’est valable que dans ces conditions. L’application à la mesure de la température de surface des océans dans un domaine très limité de longueurs d’onde constitue donc une approximation.
5° Les basses couches atmosphériques ne peuvent jouer le rôle de corps noir car elles n’en présentent aucune des caractéristiques spécifiques. Elles n’ont pas de surface, les transferts énergétiques n’y sont pas exclusivement radiatifs et elles n’absorbent ni émettent toutes les longueurs d’onde puisque les constituants atmosphériques présentent un spectre de raies en absorption comme en émission.
Le CO2 et le climat avec et sans effet de serre
De tous temps les hommes se sont intéressés au climat et ont tenté de prévoir son évolution. Dès l’Antiquité il était connu que des caractéristiques géographiques comme la latitude mais aussi l’altitude ou le voisinage de vastes étendues d’eau avaient une grande influence sur le climat. Sur cette base les climatologues ont été amenés à distinguer différents types de climats tels que tropical, désertique, tempéré, polaire, etc. Ensuite, il est progressivement apparu que le climat est un système extrêmement complexe qui dépend de l’activité solaire ainsi que de la distance et de l’orientation de la Terre par rapport au Soleil, facteurs qui varient à des échelles de temps très différentes.
Mais depuis quelques dizaines d’années, et plus particulièrement depuis la création du GIEC en 1988 sous l’égide d’organisations internationales, le climat est envisagé globalement à l’échelle de la Terre entière sans tenir compte de particularités géographiques locales. De plus, des événements singuliers tels qu’ouragans, inondations ou sécheresses sont désormais imputés par certains climatologues à un changement climatique dont l’activité humaine serait responsable. Cette théorie du changement climatique d’origine anthropique qui a des conséquences politiques, économiques et sociales très importantes repose cependant sur une seule et fragile hypothèse : le CO2 renverrait vers la Terre une partie du rayonnement qui devrait s’échapper vers le vide interplanétaire et il en résulterait une élévation de la température « moyenne globale » à la surface de la Terre. Ce phénomène radiatif improprement appelé «effet de serre » a des défenseurs et des adversaires entre lesquels le débat est souvent impossible. Il semble cependant qu’un consensus pourrait se dégager si on pouvait donner une base quantitative à certains phénomènes sur lesquels il y a accord d’un point de vue qualitatif.
1. A la recherche d’un consensus
On peut estimer que les scientifiques qui s’intéressent au climat, tant partisans qu’adversaires d’un changement climatique d’origine anthropique, s’accordent sur les points suivants :
- Le climat peut changer comme il l’a toujours fait et continuera à le faire ;
- Pour maintenir une température approximativement constante la Terre doit dissiper l’énergie reçue du Soleil et le bilan énergétique de la Terre doit tenir compte de différents mécanismes possibles ;
- Une partie de l’énergie est dissipée par la Terre sous forme de rayonnement thermique aussi qualifié de rayonnement du « corps noir » ;
- Certains gaz présents dans l’atmosphère, et notamment le CO2, peuvent absorber une fraction de ce rayonnement thermique.
- Le CO2 ayant absorbé une fraction de ce rayonnement pourrait avoir une influence sur la température de la surface terrestre ou des basses couches atmosphériques.
Poser le problème en termes quantitatifs requiert la connaissance de quelques principes de physique et de plusieurs grandeurs qui sont mal connues et ne font l’objet que d’estimations souvent contestées. Pour progresser il est cependant indispensable d’accepter certaines estimations même incertaines. Nous les considérerons alors comme hypothèses de base communes aux partisans et adversaires d’un changement climatique d’origine anthropique.
a) Quantité d’énergie solaire reçue par la Terre au sommet de l’atmosphère
Au niveau de l’orbite terrestre chaque mètre carré placé perpendiculairement au rayonnement solaire reçoit, en moyenne sur l’année, une puissance de 1368 W, c’est la « constante solaire ». La valeur de 342 W m-2 au sommet de l’atmosphère est basée sur l’idée que chaque mètre carré de la surface terrestre reçoit en continu le quart de 1368 W car la Terre n’intercepte le rayonnement solaire que sur une surface égale à celle d’un disque de même rayon. Cette valeur n’est pas mesurée mais calculée en admettant une distribution uniforme de l’énergie sur toute la surface terrestre sans tenir compte ni d’un hémisphère non éclairé, ni d’une variation en fonction de la latitude. De ce fait, elle est certainement surestimée mais une valeur correcte tenant compte de la vitesse de rotation de la Terre et de l’inclinaison de son axe de rotation donnerait lieu à des difficultés de calcul insurmontables. En attribuant à la Terre un albédo de 0,3 impliquant non seulement l’énergie réfléchie par la surface terrestre et par l’atmosphère mais aussi et principalement par les nuages, le rayonnement effectivement reçu par la surface terrestre serait alors réduit à 70 % de 342 W m-2 soit environ 240 W m-2. Acceptons cette valeur comme une première hypothèse de base commune aux partisans et adversaires d’un changement climatique d’origine anthropique.
b) Fraction d’énergie émise par la Terre sous forme de rayonnement thermique
Pour maintenir une température constante la Terre doit dissiper l’énergie reçue du Soleil par différents mécanismes : convection, évaporation de l’eau des océans et rayonnement thermique. Il subsiste une grande incertitude concernant l’importance relative de ces différents mécanismes mais le modèle le plus généralement admis est celui proposé par la NASA (voir ici). Selon la NASA 21 % de l’énergie reçue par la Terre au sommet de l’atmosphère seraient dissipés par rayonnement thermique, seul mécanisme susceptible de donner lieu à un « effet de serre ». L’évaporation de l’eau des océans et la convection de l’air interviendraient respectivement pour 23 % et 7 %. Ces proportions ne résultent pas de mesures mais d’estimations et surprennent car la convection est généralement le mécanisme prépondérant pour des objets à température et pression ambiantes tandis que le rayonnement thermique ne devient important qu’à haute température. Acceptons néanmoins le bilan thermique proposé par la NASA comme une deuxième hypothèse de base commune aux partisans et adversaires d’un changement climatique d’origine anthropique. Notons cependant que pour Sorokhtin et collaborateurs[1] la convection interviendrait pour 34 %, l’évaporation de l’eau des océans pour 13 % et le rayonnement thermique pour 4 % seulement. Finalement toute l’énergie dissipée par la surface terrestre (quel que soit le mécanisme) ou absorbée directement par l’atmosphère et les nuages est convertie en rayonnement dans les couches supérieures de l’atmosphère car c’est le seul mécanisme d’évacuation de cette énergie hors de l’atmosphère terrestre. En haute altitude les satellites détectent effectivement un rayonnement moyen de 240 W m-2, en accord avec le paragraphe 1a ci-dessus, mais les valeurs locales peuvent varier de 122 W m-2 au dessus de l’Antarctique à 265 W m-2 au dessus de la Basse Californie avec une différence de l’ordre de 50 W m-2 entre pôles et équateur. Ce rayonnement moyen provient essentiellement des couches supérieures de l’atmosphère à des températures beaucoup plus basses que la surface terrestre.
c) Fraction du rayonnement thermique de la Terre absorbée par le CO2.
En admettant que la Terre se comporte comme un corps noir à la température de 288 K (15 ° C) l’équation de Planck permet de calculer que 95 % du rayonnement thermique seraient compris entre 5 et 40 µm. Le CO2 présente une bande d’absorption dans l’infrarouge centrée à 15 µm et on trouve, en intégrant l’équation de Planck dans le domaine de 14 à 16 µm, que 9,3 % du rayonnement thermique de la Terre est émis dans cet intervalle de longueurs d’onde. On en déduit que, quel que soit son coefficient d’absorption, le CO2 ne pourrait absorber qu’un peu moins de 2 % (9,3 % de 21 %) de l’énergie totale reçue du Soleil au sommet de l’atmosphère, soit environ 6 W m-2 (voir ici). Acceptons cette valeur comme une troisième hypothèse de base commune aux partisans et adversaires d’un changement climatique d’origine anthropique. Remarquons cependant que les océans occupent 71 % de la surface terrestre et qu’il est difficile de les considérer comme corps noir puisque l’eau n’absorbe (et donc ne peut émettre) toutes les longueurs d’onde avec la même efficacité dans le domaine de 5 à 40 µm (250 à 2000 cm-1) comme l’indique la fig. 1.
d) Equilibre vibrationnel du CO2 dans les basses couches atmosphériques
A la pression d’une atmosphère et à la température de 15°C les molécules de l’air sont animées de mouvements de translation à des vitesses de l’ordre de 500 m par seconde. Dans ces conditions chacune subit plusieurs milliards de collisions par seconde (voir ici ). Si elles disposent de l’énergie suffisante elles peuvent aussi entrer en vibration avec variation rapide et périodique des longueurs ou des angles de leurs liaisons interatomiques. Les molécules biatomiques N2 et O2 sont très rigides et ne vibrent pratiquement pas à 15°C. Par contre, les molécules triatomiques de CO2, linéaires à l’état fondamental O=C=O, peuvent se déformer facilement et devenir anguleuses en vibrant. L’énergie requise pour atteindre cet état de vibration peut être calculée à partir de la bande d’absorption détectée à 15 µm dans le spectre infrarouge du CO2 grâce à la relation Ev = hc/λ (où h est la constante de Planck, c la vitesse de la lumière et λ la longueur d’onde du rayonnement absorbé, dans ce cas 15 µm). Cette valeur n’est que de 30 % supérieure à l’énergie cinétique moyenne des molécules environnantes N2 et O2 qui, d’après la théorie cinétique des gaz, vaut Ec = 5/2 k T (où k est la constante de Boltzmann et T la température en Kelvin). Or, beaucoup de molécules ont une énergie cinétique supérieure à cette valeur moyenne car les énergies cinétiques de translation Et = mv2/2 présentent une large distribution continue qui suit la statistique de Maxwell-Boltzmann. La fonction mathématique correspondante permet de calculer qu’à 15°C plus de 40 % des molécules N2 et O2 ont suffisamment d’énergie cinétique pour amener les molécules de CO2 à leur plus bas niveau de vibration lors d’une collision inélastique (sans conservation de l’énergie cinétique). On admet généralement que 0,001 % des collisions sont inélastiques (voir 2c ci-dessous) ce qui représente encore plusieurs dizaines de milliers par seconde. Dans ces conditions il y a conversion d’une fraction ∆ de l’énergie cinétique de translation des molécules N2 ou O2 en énergie de vibration du CO2 :
∆Ec (translation) de N2 + CO2 ↔ ∆Ev (vibration) de CO2 + N2
Cette conversion est réversible et les molécules de CO2 excitées se désactivent endéans quelques microsecondes pour retourner à l’état fondamental lors de nouveaux chocs avec les molécules environnantes qui, de ce fait, acquièrent temporairement un surcroît d’énergie cinétique de translation. Il existe donc un équilibre dynamique résultant des très nombreuses collisions. Il ne dépend que de la température et de la pression (par le biais de la distribution des énergies et du nombre de chocs entre molécules). Quoique ce ne soient pas toujours les mêmes molécules de CO2 qui vibrent la proportion de molécules en état de vibration reste constante à une température et une pression déterminées (environ 40% à 15°C et à la pression d’une atmosphère). Admettons le transfert d’énergie entre molécules de CO2 et molécules environnantes comme quatrième hypothèse de base commune aux partisans et adversaires d’un changement climatique d’origine anthropique.
A ce stade de la discussion si les quatre points ci-dessus font l’objet d’un large consensus entre partisans et adversaires d’un changement climatique d’origine anthropique leur divergence d’opinion pourrait donner lieu un véritable débat scientifique. Cette divergence d’opinion se manifeste fondamentalement à propos du mécanisme de désactivation des molécules de CO2 excitées par absorption d’une fraction du rayonnement thermique de la Terre. Envisageons successivement avec le maximum d’objectivité les arguments scientifiques présentés par les uns et les autres.
2. Influence du CO2 sur le climat
Les partisans de la théorie du changement climatique d’origine anthropique invoquent à l’appui de leur thèse l’existence d’un « effet de serre » alors que leurs adversaires contestent cette hypothèse. Avant toute discussion il est essentiel d’en bien définir le sujet, en l’occurrence l’effet de serre.
a) Définition de l’effet de serre
Il existe un grand nombre de définitions de l’effet de serre. Gerlich et Tscheuschner en rappellent plus d’une demi-douzaine (voir paragraphe 3.3 ici) qui, pour la plupart, résultent d’une mauvaise compréhension du phénomène qui intervient réellement dans une serre agricole. Certains média destinés au grand public font appel à une analogie naïve en prétendant que les gaz à effet de serre entourent la Terre « comme une couverture » et l’empêchent de perdre sa chaleur. La seule définition de l’effet de serre qui décrit clairement le phénomène envisagé et répond, de plus, au critère de réfutabilité énoncé par Popper est la suivante :
« L’effet de serre est un phénomène radiatif causé par des gaz tels la vapeur d’eau ou le CO2 qui absorbent une fraction du rayonnement infrarouge émis par la Terre et le réémettent ensuite dans toutes les directions et notamment vers la surface terrestre dont la température serait, de ce fait, plus élevée qu’en l’absence de gaz absorbant l’infrarouge. Ces gaz sont dès lors qualifiés de gaz « à effet de serre ».
Considérons cet énoncé comme une définition scientifique acceptable tant par les partisans que par les adversaires d’un changement climatique d’origine anthropique.
b) Influence du CO2 sur le climat avec effet de serre.
L’argument le plus souvent avancé par les partisans de la théorie du changement climatique d’origine anthropique est qu’en l’absence de gaz à effet de serre la température « globale moyenne » de la Terre serait de – 18°C au lieu de la température généralement admise de 15 °C. En réalité cette différence de 33 °C, parfois présentée même comme une définition de l’effet de serre, est basée sur un calcul incorrect. En effet, la température de – 18°C est obtenue en introduisant dans la formule de Stefan-Boltzmann la valeur de 240 W m-2 mesurée par satellite (voir 1b ci-dessus). Or, la formule de Stefan-Boltzmann n’est valable que si le rayonnement thermique est le seul mécanisme d’échange énergétique (voir ici). Cette valeur de – 18°C correspondrait donc à une Terre sans atmosphère et non sans gaz à effet de serre. Mais sans atmosphère l’albédo de la Terre serait voisin de 0,1 (comme celui de la Lune) et non 0,3 valeur due largement à la présence de nuages (voir 1a ci-dessus). Avec un albédo de 0,1 la quantité d’énergie reçue par la Terre en provenance du Soleil puis réémise serait 308 W m-2 et non 240 W m-2. L’application, justifiée cette fois, de la formule de Stefan-Boltzmann conduirait à une température de 271 K (soit – 2°C) pour une Terre sans atmosphère. La différence de 17°C entre cette valeur théorique et la température « moyenne globale» de la Terre est due à la présence d’une atmosphère qui modifie le mécanisme de dissipation de l’énergie par comparaison avec une Terre sans atmosphère.
Dans le cas d’un gaz parfaits à l’équilibre hydrostatique, la thermodynamique de l’atmosphère (www.lmd.jussieu.fr/~fcodron/COURS/notes_thermo.pdf) conduit à la relation :
dQ = Cp dT + g dh
où Cp est la capacité thermique massique de l’air et g l’accélération due à la pesanteur
En absence d’échange avec l’environnement dQ = 0 d’où dT = – g/Cp .dh et en intégrant on trouve :
T – T0 = – (g /Cp) (h –ho)
Dans cette formule ho est une altitude de référence où la température vaut To. Le facteur g/Cp est appelé gradient adiabatique (« lapse rate » en anglais). Cette formule indique que la température diminue linéairement lorsque l’altitude augmente. Avec g = 9,8 m s-2 et Cp = 1005 J kg-1 K-1 pour l’air sec on trouve un gradient adiabatique de 9,75 K/km, ordre de grandeur généralement admis en atmosphère sèche. La capacité thermique massique de l’air humide étant plus élevée le gradient adiabatique sera plus faible et dépendra de la température. Une valeur « environnementale moyenne » de 6,5 K/km est prise en compte par l’International Civil Aviation Organization (ICAO). Sur cette base en prenant la température de 15° C comme référence au niveau de la mer on calcule que la température souvent citée de – 18°C serait atteinte à une altitude de 5100 m. La différence de 33° C observée par rapport à 15° C est évidemment due à la différence d’altitude comme l’indique la formule ci-dessus et ne peut être considérée comme la manifestation d’un effet de serre.
La présence d’une atmosphère ne réchauffe évidemment pas la Terre. Ce sont les basses couches atmosphériques qui sont réchauffées au contact du sol chauffé par le Soleil et le gradient adiabatique fait que l’air se refroidit progressivement avec l’altitude donnant lieu à un courant de convection. Cet effet ne dépend en rien de la présence d’un peu de CO2 dans l’air.
Si les 2 % de l’énergie solaire absorbés par le CO2 à partir du rayonnement thermique de la Terre (voir 1c ci-dessus) sont réémis dans toutes les directions il n’y en aurait pas plus de la moitié qui atteindrait la surface terrestre soit environ 3 W m-2. Pour fixer un ordre de grandeur rappelons qu’un être humain au repos dissipe 60 à 100 W sous forme de chaleur. L’augmentation de température due à un éventuel effet de serre serait donc bien inférieure à celle résultant de la présence d’un être humain occupant une surface d’un mètre carré. Encore faudrait-il que la surface terrestre puisse réabsorber spécifiquement le rayonnement de longueur d’onde 15 µm d’abord émis par la surface terrestre puis absorbé par le CO2 et finalement réémis. Ce serait en contradiction avec l’hypothèse que la Terre se comporte comme un corps noir (ou gris) qui, à l’équilibre thermique, ne peut pas absorber plus d’énergie qu’il n’en émet (voir ici ). On pourrait objecter que les océans qui occupent 71 % de la surface terrestre ne se comportent pas comme un corps noir (ou gris). En effet, l’eau liquide présente une large bande d’absorption centrée à 14,8 µm (675 cm-1). Connaissant le coefficient d’absorption de cette bande (voir fig. 1) on peut calculer que l’absorption d’un rayonnement de longueur d’onde 15 µm serait pratiquement totale sur une épaisseur de 15 microns. L’absorption d’énergie par cette couche très superficielle ne pourrait évidemment contribuer au réchauffement des océans.

Fig. 1 Spectre d’absorption de l’eau liquide dans le domaine de l’infrarouge thermique
On peut en conclure que l’effet de serre, s’il existait, ne pourrait conduire à un réchauffement de la surface terrestre émergée mais seulement à un léger accroissement du mécanisme de dissipation de l’énergie par évaporation de l’eau des océans au détriment du rayonnement thermique.
c) Influence du CO2 sur le climat sans effet de serre
Le principal argument qui conduit à réfuter la théorie de l’effet de serre est que la probabilité de désactivation radiative du CO2 ayant absorbé une fraction du rayonnement thermique de la Terre est pratiquement nulle car l’équilibre vibrationnel mentionné en 1d ci-dessus ne dépend que de la température et de la pression. La fraction de molécules à l’état de vibration restera donc voisine de 40 % à des pressions voisines d’une atmosphère et à la température de 15 °C, quelle que soit la quantité d’énergie absorbée à partir du rayonnement thermique de la Terre car cet apport d’énergie supplémentaire sera rapidement converti en énergie de translation des molécules environnantes.
La conversion d’énergie de vibration en énergie de translation (V → T) est un phénomène bien connu dont l’étude s’est développée grâce aux progrès de la technologie laser permettant d’obtenir sélectivement différents états de vibration [2]. En particulier la désactivation par collisions de molécules de CO2 à leur plus bas niveau énergétique de vibration ( notées CO2*) a été bien étudiée et les constantes de vitesse de la réaction :
CO2* + N2 (ou O2) → CO2 + N2 (ou O2)
ont été mesurées entre 300 et 140 K [3]. Elles sont de l’ordre de 105 fois inférieures à ce que l’on aurait pu prévoir sur la base du nombre total de collisions (plusieurs milliards par seconde) car elles résultent seulement des collisions inélastiques qui ne représentent, en général, que 0,001 % du nombre total de collisions. D’autre part, la conversion inverse d’énergie de translation en énergie de vibration (T → V) a aussi été étudiée dans le cas du CO2. A des altitudes de l’ordre de 100 km l’énergie de translation d’atomes d’oxygène peut être transférée à des molécules de CO2 et convertie en énergie de vibration [4] :
O + CO2 → O + CO2*
A cette altitude la pression est si faible que le nombre de collisions entre molécules n’est plus que de l’ordre de 1000 par seconde et une fraction des molécules de CO2* peut alors se désactiver avec émission d’un rayonnement de longueur d’onde λ =15 µm:
CO2* → CO2 + Ev ( = hc/λ)
On attribue à cette réaction un effet de refroidissement de l’atmosphère par conversion d’énergie cinétique en rayonnement [5].
Ces exemples confirment qu’à 15° C et à des pressions voisines d’une atmosphère les molécules de CO2 en état de vibration se désactiveront par collisions avec les molécules environnantes comme mentionné au paragraphe 1d ci-dessus. Dans ces conditions régnant à la surface de la Terre l’effet de serre ne peut avoir lieu. La désactivation radiative d’un état excité ne peut entrer en compétition avec la désactivation par collisions que pour des états excités de très courte durée de vie (10-9 à 10-7s) qui peuvent émettre un rayonnement avant qu’une collision inélastique ne se produise. C’est le cas de nombreuses molécules organiques complexes dont la fluorescence est observée en solution. La désactivation radiative est aussi possible si la fréquence des collisions intermoléculaires est très faible (en milieu gazeux à très faible pression comme dans l’exemple ci-dessus ou en milieu vitreux rigide). Ces résultats permettent de conclure que les molécules de CO2 excitées à l’état de vibration par absorption d’une fraction du rayonnement thermique de la Terre se désactiveront selon le mécanisme mentionné au paragraphe 1d ci-dessus et l’apport d’énergie supplémentaire sera rapidement converti en énergie de translation des molécules environnantes ce qui aura pour effet d’augmenter les mouvements de convection qui contribuent à dissiper l’énergie solaire absorbée par la surface terrestre.
3. Conclusion
De cet exposé on peut conclure que l’effet de serre, tel que défini en 2a ci-dessus, n’existe pas au niveau des basses couches atmosphériques et que, même s’il existait, l’apport d’énergie résultant de l’absorption d’une fraction du rayonnement thermique de la Terre serait rapidement converti en évaporation de l’eau des océans. Par contre, en l’absence d’effet de serre ce sont les mouvements de convection de l’air qui sont légèrement accentués. Dans l’un et l’autre cas le bilan énergétique global de la Terre ne sera pas modifié puisque finalement toute l’énergie dissipée par la surface terrestre, quel que soit le mécanisme, est convertie en rayonnement dans les couches supérieures de l’atmosphère car c’est le seul mécanisme d’évacuation de cette énergie hors de l’atmosphère terrestre (voir 1b ci-dessus). L’improbable débat entre partisans et adversaires d’un changement climatique d’origine anthropique pourrait donc être rapidement clôturé puisque le CO2 ne peut contribuer en aucune manière à un réchauffement de la surface terrestre.
Le réchauffement climatique d’origine anthropique
Le climat peut changer, comme il l’a toujours fait et continuera à le faire sous l’action de variables naturelles. Les activités humaines peuvent-elles avoir une influence comme le prétend la théorie du réchauffement climatique d’origine anthropique ? Cette théorie est basée sur l’existence d’un hypothétique effet de serre défini comme un phénomène radiatif causé par des gaz tels la vapeur d’eau ou le CO2 qui absorbent une fraction du rayonnement infrarouge émis par la Terre et le réémettent ensuite dans toutes les directions et notamment vers la surface terrestre dont la température serait, de ce fait, plus élevée qu’en l’absence de gaz absorbant l’infrarouge. L’effet de serre résulterait donc essentiellement de l’émission par les molécules de CO2 d’un rayonnement de fluorescence dans le domaine infrarouge[1]. Cette définition est claire et scientifiquement valable car conforme au principe de réfutabilité défini par Karl Popper. Nous l’examinerons à la lumière de théories physiques bien établies et de faits expérimentaux connus.
1. Le CO2 dans les basses couches atmosphériques
Oublions tout d’abord le climat et envisageons une boîte opaque contenant, à l’abri de tout rayonnement extérieur, une certaine quantité d’air sec à 15°C et à la pression d’une atmosphère. Dans cette boîte 78 % des molécules sont des molécules d’azote N2 et 21 % sont des molécules d’oxygène O2. Le troisième constituant par ordre d’abondance est l’argon Ar (environ 1 % des molécules). Les molécules de CO2 n’interviennent que pour environ 0,04 %. Toutes ces molécules n’ont pratiquement pas d’interaction entre elles, si ce n’est qu’étant en constante agitation elles entrent en collisions les unes avec les autres lors de chocs dont la plupart sont élastiques (avec conservation de l’énergie cinétique).
1a) Energie de translation
La théorie cinétique des gaz permet de calculer qu’à la température de 15°C les molécules de l’air sont animées de vitesses de translation de l’ordre de 500 m par seconde et qu’à la pression d’une atmosphère, chacune subit plusieurs milliards de collisions par seconde. Ces molécules présentent une large distribution de vitesses qui est fonction de la température en accord avec la loi de Maxwell-Boltzmann (fig.1). L’énergie cinétique moyenne des molécules biatomiques N2 et O2 peut être calculée et vaut Em = 5/2 k T (où k est la constante de Boltzmann et T la température en Kelvin).

1b) Energie de vibration
Les molécules de l’air ne sont pas seulement animées de mouvements de translation. Si elles disposent de l’énergie suffisante elles peuvent aussi entrer en vibration avec variation rapide et périodique des longueurs ou des angles de leurs liaisons interatomiques. Les molécules biatomiques N2 et O2 sont très rigides et ne vibrent pratiquement pas à 15°C. Par contre, les molécules triatomiques de CO2, linéaires à l’état fondamental O=C=O, peuvent se déformer facilement et devenir anguleuses en vibrant. A chaque fréquence de vibration est associée une énergie et la théorie quantique nous enseigne que toutes les fréquences de vibration ne sont pas permises. Seuls certains niveaux énergétiques existent dont l’énergie peut être déterminée expérimentalement par spectroscopie d’absorption dans le domaine infrarouge ou Raman. Ainsi l’énergie associée à la vibration de déformation du CO2 peut être calculée à partir de la bande d’absorption détectée à 15 µm dans le spectre infrarouge de la molécule grâce à la relation Ev = hc /λ (où h est la constante de Planck, c la vitesse de la lumière et λ la longueur d’onde du rayonnement absorbé, dans ce cas 15 µm). Cette valeur n’est que de 30 % supérieure à Em l’énergie cinétique moyenne des molécules environnantes N2 et O2 mentionnée dans le paragraphe précédent. Or, beaucoup de ces molécules ont une vitesse supérieure à la moyenne comme l’indique la fig. 1 (la vitesse moyenne est très proche du maximum de la courbe de distribution des vitesses) et donc aussi une énergie cinétique Ec supérieure à la moyenne.
1c) Conversion d’énergie de translation en énergie de vibration et inversement
En l’absence d’une source extérieure de rayonnement l’énergie nécessaire pour exciter la vibration de CO2 ne peut provenir que de l’agitation thermique du milieu ambiant. La quantification de l’énergie n’intervient pas au niveau des mouvements de translation et les énergies cinétiques de translation Ec = mv2/2 présentent une large distribution continue semblable à celle illustrée sur la fig. 1. La fonction mathématique correspondant à ces courbes permet de calculer qu’à 15°C plus de 40 % des molécules N2 et O2 ont une énergie cinétique Ec supérieure à l’énergie Ev du plus bas niveau de vibration des molécules de CO2. Elles peuvent donc l’amener à ce niveau lors d’une collision inélastique (sans conservation de l’énergie cinétique). Dans ces conditions il y a conversion d’une fraction ∆ de l’énergie cinétique de translation des molécules N2 ou O2 en énergie de vibration d’une fraction des molécules de CO2 :
∆Ec (translation) de N2 + CO2 → ∆Ev (vibration) de CO2 + N2 (1)
Ce ne sont évidemment pas toujours les mêmes molécules de CO2 qui sont en état de vibration car cette conversion est réversible et les molécules se désactivent endéans quelques millisecondes pour retourner à l’état fondamental lors de nouveaux chocs avec les molécules environnantes qui, de ce fait, acquièrent temporairement un surcroît d’énergie cinétique de translation :
∆Ev (vibration) de CO2 + N2 → ∆Ec (translation) de N2 + CO2 (2)
Il existe donc un équilibre dynamique associé aux réactions (1) et (2) qui sont l’inverse l’une de l’autre. Cet équilibre ne dépend que de la température et de la pression (par le biais de la distribution des énergies et du nombre de chocs entre molécules). Quoique ce ne soient pas toujours les mêmes molécules de CO2 qui vibrent, la proportion de molécules en état de vibration reste constante à une température et une pression déterminées (environ 40 % à 15°C à la pression d’une atmosphère). Cet équilibre ne sera pas modifié si, en plus, certaines molécules de CO2 sont excitées par absorption d’une fraction du rayonnement infrarouge émis par la Terre. On peut donc en conclure que la désactivation des molécules de CO2 ne se fera pas avec émission d’un rayonnement. La raison en est qu’à des pressions voisines d’une atmosphère la fluorescence ne pourrait entrer en compétition avec la désactivation par collisions que pour des états excités de très courte durée de vie (10-9 à 10-7 s) qui pourraient se désactiver par fluorescence avant qu’un nombre suffisant de collisions avec les molécules environnantes n’intervienne. Or, la durée de vie du plus bas état excité de CO2 étant 0,64 s[2] des millions de collisions interviendront avant que l’émission d’un rayonnement ne puisse avoir lieu. L’hypothèse de l’effet de serre est donc sans fondement théorique.
Note complémentaire basée sur des résultats expérimentaux
La conversion d’énergie de vibration en énergie de translation (V → T) et d’ énergie de translation en énergie de vibration (T → V) comme dans les réactions (1) et (2) est un phénomène bien connu dont l’étude s’est développée grâce aux progrès de la technologie laser permettant d’obtenir sélectivement différents états de vibration[3]. En particulier, la conversion d’énergie de vibration en énergie de translation (V → T) a été étudiée dans le cas de molécules de CO2 excitées par laser au plus bas état de vibration. Les constantes de vitesse de la réaction :
CO2* + N2 (ou O2) → CO2 + N2 (ou O2)
ont été mesurées entre 300 et 140 K[4]. Elles sont de l’ordre de 105 fois inférieures à celles prévues sur la base du nombre de collisions (plusieurs milliards par seconde) car elles résultent seulement des collisions inélastiques qui ne représentent que 0,001 % du nombre total de collisions. D’autre part, la conversion d’énergie de translation en énergie de vibration (T → V) a aussi été étudiée dans le cas du CO2. A des altitudes de l’ordre de 100 km l’énergie cinétique de translation d’atomes d’oxygène peut être transférée à des molécules de CO2 et convertie en énergie de vibration[5] :
O + CO2 → O + CO2*
Le phénomène a été mis en évidence en détectant la fluorescence (désactivation radiative) des molécules de CO2 avec émission d’un rayonnement de longueur d’onde λ = 15 µm :
CO2* → CO2 + hc / λ
A ces altitudes la pression atmosphérique est si faible que le nombre total de collisions entre molécules n’est plus que de l’ordre de 1000 par seconde. Une fraction des molécules de CO2 excitées peut alors se désactiver avec émission d’un rayonnement avant qu’une collision inélastique ne se produise avec les molécules environnantes. Ce n’est pas le cas dans les basses couches atmosphériques où l’émission d’un rayonnement de fluorescence du CO2 n’a jamais été observée. L’hypothèse de l’effet de serre invoquée par les partisans d’un réchauffement climatique d’origine anthropique n’a donc aucune justification ni théorique, ni expérimentale.
2. Le bilan énergétique de la Terre
Pour estimer la fraction du rayonnement thermique de la Terre qui pourrait être absorbée par le CO2 il faut envisager le bilan énergétique de la Terre qui est basé sur l’idée que pour maintenir une température constante la Terre doit dissiper par différents mécanismes l’énergie reçue du Soleil. Le modèle le plus souvent cité est celui proposé par la NASA (fig. 2).

D’après ce bilan 30 % de l’énergie reçue par la Terre au sommet de l’atmosphère seraient réfléchis par les nuages, l’atmosphère et la surface terrestre en accord avec un albédo de 0,3. L’atmosphère et les nuages absorberaient en plus 19 % du rayonnement solaire transmis et finalement 51 % seulement seraient absorbés par les continents et les océans. Cette énergie serait dissipée ensuite par trois mécanismes distincts : évaporation de l’eau des océans (23 %), convection de l’air (7 %) et rayonnement thermique (21 %). Remarquons tout d’abord que le bilan présenté sur la fig.2 ne fait apparaître aucune « back radiation » associée à un éventuel effet de serre. Une petite fraction seulement du rayonnement détecté par satellite provient directement de la surface terrestre (fine flèche rouge à droite sur la fig. 2) car émise dans la zone de transparence atmosphérique entre 8 à 13 µm (fig.3). En intégrant l’équation de Planck pour un corps noir à 15°C dans le domaine de 8 à 13 µm on calcule que 30 % du rayonnement thermique de la Terre est émis dans cette zone de transparence atmosphérique soit env. 6 % de l’énergie totale reçue du Soleil au sommet de l’atmosphère terrestre. Le reste du rayonnement thermique émis par la Terre est absorbé par divers constituants atmosphériques (fig. 3) principalement la vapeur d’eau mais aussi le CO2 . Quel que soit le mécanisme de dissipation de l’énergie au niveau de la surface terrestre, en altitude toute cette énergie doit être convertie en rayonnement car c’est le seul mécanisme permettant de l’évacuer hors du système terrestre (large flèche rouge sur la fig.2)

(les zones de transparence apparaissent en bleu, notamment entre 8 à 13 µm)
Les proportions mentionnées dans le bilan énergétique de la NASA ne résultent le plus souvent que d’estimations. Elles sont d’ailleurs assez surprenantes car la convection est généralement le mécanisme prépondérant pour des objets à température et pression ambiantes tandis que le rayonnement thermique ne devient important qu’à haute température. Dans cette optique Sorokhtin et collaborateurs [5] considèrent que la convection serait effectivement le mécanisme prépondérant intervenant pour 34 % tandis que le rayonnement thermique interviendrait seulement pour 4 % et l’évaporation de l’eau des océans pour 13 %. Il subsiste donc une très grande incertitude concernant l’importance relative de ces trois mécanismes.
Au niveau de l’orbite terrestre chaque mètre carré placé perpendiculairement au rayonnement solaire reçoit, en moyenne sur l’année, une puissance de 1368 W, c’est la « constante solaire ». La valeur moyenne de 342 W m-2 au sommet de l’atmosphère est basée sur l’idée que chaque mètre carré de la surface terrestre reçoit en continu le quart de 1368 W car la Terre n’intercepte le rayonnement solaire que sur une surface égale à celle d’un disque de même rayon. Cette valeur n’est pas mesurée mais calculée en admettant une distribution uniforme de l’énergie sur toute la surface terrestre sans tenir compte ni d’un hémisphère non éclairé, ni d’une variation en fonction de la latitude. De ce fait, elle est certainement surestimée. De plus, si la distribution de l’énergie était uniforme il n’y aurait ni saisons, ni courants marins ou aériens qui sont cependant des éléments déterminants du climat. Néanmoins, cette valeur approximative est généralement adoptée car une valeur correcte tenant compte de la vitesse de rotation de la Terre et de l’inclinaison de son axe de rotation donnerait lieu à des difficultés de calcul insurmontables. Ensuite, en attribuant à la Terre un albédo de 0,3 impliquant non seulement l’énergie réfléchie par la surface terrestre et par l’atmosphère mais aussi et principalement par les nuages, le rayonnement effectivement reçu par la surface terrestre serait réduit à 70 % de 342 W m-2 soit environ 240 W m-2. En haute altitude les satellites détectent effectivement un rayonnement moyen de 240 W m-2 avec une différence de l’ordre de 50 W m-2 entre pôles et équateur. Ce rayonnement moyen provient essentiellement des couches supérieures de l’atmosphère à des températures beaucoup plus basses que celle de la surface terrestre et on ne peut en déduire, sur base de la formule de Stefan-Boltzmann, que la surface terrestre devrait avoir la température de – 18° C (voir ici).
Si on considère la Terre comme un corps noir à 15°C l’équation de Planck (voir ici) permet de calculer que 95 % du spectre d’émission sera compris entre 5 et 40 µm et la loi de Wien prévoit que le rayonnement émis devrait présenter un maximum d’intensité à 10 µm. Le CO2 présente une bande d’absorption dans le domaine du rayonnement thermique de la Terre. Elle est présentée sur la fig. 4 pour une teneur en CO2 de 357 ppm (0,0357 %) en présence de 2,6 % en vapeur d’eau, conditions correspondant à la composition atmosphérique en 1993.

La bande d’absorption centrée à 15 µm permet l’excitation de la molécule à son plus bas niveau de vibration impliquant une déformation angulaire. Les branches P et R sont dues à l’existence de sous-niveaux de rotation pour chaque niveau de vibration (fondamental et excité). En intégrant l’équation de Planck de 14 à 16 µm, domaine d’absorption du CO2, on calcule que 9,3 % du rayonnement thermique de la Terre sont émis dans cet intervalle de longueurs d’onde. En fin de compte le CO2, quel que soit son coefficient d’absorption, ne pourrait absorber au maximum que 9,3 % du rayonnement thermique de la Terre (représentant, selon la NASA, 21 % de l’énergie totale reçue du Soleil au sommet de l’atmosphère) soit un peu moins de 2 % de 342 W m-2 donc environ 7 W m-2 . Pour Sorokhtin et collaborateurs [5], le rayonnement thermique de la Terre représentant seulement 4 % de l’énergie totale reçue du Soleil, le CO2 n’absorberait donc au maximum qu’un peu moins de 0,4 % de 342 W m-2 soit environ 1,3 W m-2.
Les molécules de CO2 excitées à l’état de vibration par absorption d’une fraction du rayonnement thermique de la Terre se désactivent endéans quelques microsecondes par collisions avec les molécules environnantes, principalement N2 et O2. Dans ces conditions, il y a conversion de l’énergie de vibration du CO2 en énergie cinétique de translation des molécules N2 ou O2 selon la réaction (2) mentionnée au paragraphe 1c. Bien que l’absorption du rayonnement thermique de la Terre entre 14 et 16 µm soit sélective par les molécules de CO2 cet excédent d’énergie se répartira sur l’ensemble des molécules environnantes suite aux multiples collisions. Au total, selon les auteurs 0,4 % ou 2 % de l’énergie reçue du Soleil au sommet de l’atmosphère terrestre seront convertis en mouvements de convection au détriment de l’intensité du rayonnement thermique dont une fraction est absorbée par le CO2. La présence de CO2 dans l’atmosphère ne modifie donc pas le bilan énergétique global de la Terre mais seulement l’importance relative des différents mécanismes de dissipation de l’énergie reçue du Soleil. Cela ne peut avoir aucune influence sur la température « globale moyenne » de la surface terrestre.
3. Influence du CO2
En l’absence d’effet de serre la conversion de l’énergie de vibration du CO2 en énergie cinétique de translation des molécules de N2 et O2 pourrait-elle avoir un effet sur la température des basses couches atmosphériques ? Pour estimer l’importance d’un tel effet il faudrait connaître le volume d’air dans lequel cette énergie sera dissipée. En utilisant la relation de Beer-Lambert avec Io = intensité incidente et I = intensité transmise :
log Io/I = A C L
et en y introduisant des valeur A = 20,2 m2/mol pour le coefficient d’absorption molaire du CO2[7] et C = 1,78 10-2 mol m-3 (pour 0,04 % de CO2 en volume) on trouve que log Io/I vaut 3 (99,9 % d’absorption) pour une épaisseur atmosphérique L = 8 m. Connaissant le nombre de molécules dans une colonne d’air de 8 m de hauteur et de 8 m3 de volume dans lequel seront dissipés 1,3 ou 7 W (selon les auteurs) on trouve que l’énergie cinétique moyenne Em des molécules N2 et O2, calculée au paragraphe 1a, n’augmenterait en une seconde que d’environ 0,0001 % . Cette valeur ne sert qu’à fixer un ordre de grandeur car il n’y a évidemment pas d’accumulation d’énergie cinétique au cours du temps puisqu’un important courant de convection existe déjà. Le gradient de température existant déjà dans les basses couches atmosphériques ne sera donc pas affecté par la présence de CO2.
Le coefficient d’absorption molaire utilisé correspond seulement à la branche Q, la plus importante du spectre d’absorption (fig.4). Pour les branches P et R qui présentent des coefficients d’absorption environ 10 fois moindres l’absorption de 99,9 % du rayonnement thermique de la Terre nécessiterait une épaisseur atmosphérique environ 10 fois plus importante et le transfert d’énergie se fera sur un nombre de molécules environ 10 fois plus grand avec un effet réduit proportionnellement. Notons encore que ces conclusions s’appliquent à la totalité du CO2 présent dans l’atmosphère (0,04 %) qu’il soit d’origine naturelle ou humaine. Or, de nombreux travaux récents montrent que la teneur en CO2 d’origine anthropique ne serait que d’environ 5 % (voir ici)
4. Conclusion
De cet exposé on peut conclure que :
1° L’effet de serre, qui résulterait de la désactivation radiative (fluorescence) de molécules ayant absorbé une fraction du rayonnement thermique de la Terre, ne peut exister au niveau des basses couches atmosphériques.
2° Au niveau des basses couches atmosphériques, les molécules ayant absorbé une fraction du rayonnement thermique de la Terre se désactivent par collisions avec les molécules environnantes principalement N2 et O2.
3° La conversion d’énergie de vibration des molécules de CO2 en énergie de translation des molécules environnantes ne modifie pas le bilan énergétique global de la Terre.
4° Le CO2 ne peut contribuer en aucune manière à un réchauffement ni de la surface terrestre ni des basses couches atmosphériques.
5° La théorie du réchauffement climatique d’origine anthropique basée sur l’existence d’un effet de serre n’a aucune justification ni théorique ni expérimentale.
Références
L’effet de serre et le bilan énergétique de la Terre
Dans presque toutes les sciences, les notions élémentaires sont les plus difficiles et elles sont parfois mal comprises. Par la suite, elles sont souvent négligées car elles ne s’opposent pas à la publication d’articles dans des domaines spécialisés où les auteurs, à la recherche de notoriété ou de subsides, sont jugés par leurs pairs. La climatologie, science récente et pluridisciplinaire par essence, n’échappe pas à cette règle. C’est ainsi que beaucoup de climatologues, réputés tels ou simples amateurs, développent des théories dont les hypothèses sont contraires aux principes fondamentaux de la chimie et de la physique. Néanmoins, sur la base de ces théories mal étayées, des modèles informatiques sont élaborés qui conduisent, avec une précision rassurante, à des prévisions alarmantes. Dans cette note nous rappellerons d’abord quelques notions élémentaires concernant l’émission et l’absorption de rayonnements par la Terre et par les gaz atmosphériques avant de revoir d’un point de vue critique les notions généralement admises à propos de l’effet de serre et du bilan énergétique de la Terre.
1. Deux types de rayonnement à ne pas confondre
1.1. Émission de rayonnement thermique
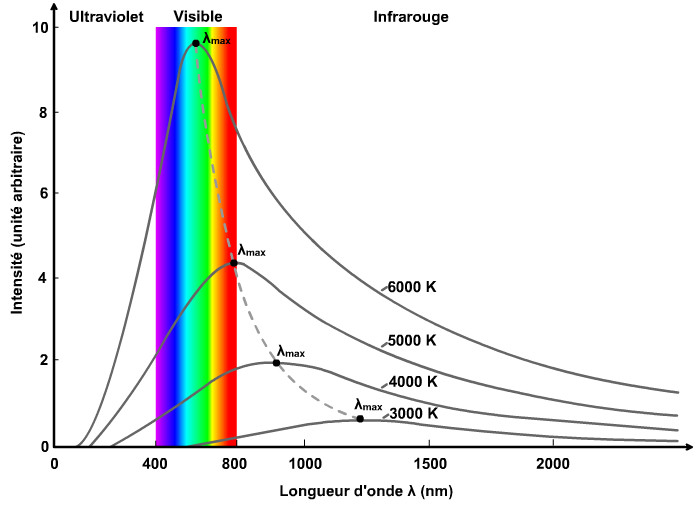
Tout corps solide à une température supérieure au zéro absolu émet un rayonnement qui apparaît dans le domaine visible pour des températures supérieures à 3000 K mais se limite principalement au domaine infrarouge pour des températures inférieures (fig. 1). Ce rayonnement qualifié de « thermique » se présente toujours sous forme d’un spectre continu avec une forte variation d’intensité du côté des courtes longueurs d’onde (hautes énergies), passage par un maximum à la longueur d’onde λmax qui se déplace en fonction de la température (comme indiqué sur la fig. 1) et perte progressive d’intensité du côté des grandes longueurs d’onde (faibles énergies). Il est dû à l’oscillation de dipôles électriques formés par le noyau et le nuage électronique des atomes qui, en accord avec les lois de l’électromagnétisme, émettent un rayonnement de fréquence égale à la fréquence d’oscillation.
Dans la seconde moitié du 19ème siècle plusieurs physiciens ont tenté d’élaborer une théorie du « corps noir », objet idéal qui, à l’équilibre thermique, absorbe et émet toutes les longueurs d’onde d’où la qualification de « noir ». Ce n’est qu’en 1900 que Planck proposa une équation introduisant l’idée, révolutionnaire pour l’époque, qu’à chaque longueur d’onde le rayonnement ne peut être émis que sous forme de « quanta » (c’est-à-dire de petits paquets) dont l’énergie est hν = hc/λ (où ν et λ sont respectivement la fréquence et la longueur d’onde du rayonnement émis, c la vitesse de la lumière et h une nouvelle constante de la nature appelée désormais constante de Planck). Cette formule, ainsi que quelques limitations à son usage, est rappelée dans une note publiée sur ce site (http://www.science-climat-energie.be/2018/04/26/du-bon-usage-de-la-formule-de-stefan-boltzmann/). L’intégration de l’équation de Planck sur tout le domaine de longueurs d’onde conduit à la formule de Stefan-Boltzmann qui lie l’émittance hémisphérique (à 180°dans toutes les directions à partir d’une surface) E(T) (en W m-2) à la température T (en K) à la puissance 4 :
E (T) = σ T4 (σ = constante de Stefan = 5,67 x 10-8 W m-2 K-4) (1)
La relation (1) fournit une mesure de l’aire sous les courbes de la fig. 1. Il faut remarquer que l’émittance hémisphérique intervenant dans la relation (1) est fondamentalement différente du flux « unidirectionnel » (ascendant ou descendant) F(T) de la relation (2) qui est l’outil de travail par excellence des climatologues :
F (T) = σ T4 (2)
Cette dernière relation, bien que couramment utilisée, doit donc être considérée comme une approximation. La fig. 1 montre aussi que le maximum de la courbe d’émission se déplace avec la température selon la loi de Wien :
λmax = C / T (C = 2,9 10-3 m K) (3)
L’intégration de l’équation de Planck permet de calculer que 95 % de l’émission thermique d’un corps noir se situe dans le domaine de longueurs d’onde s’étendant de 0,5. λmax à 4. λmax
Les caractéristiques essentielles d’un rayonnement thermique sont que :
- – le spectre d’émission est continu, son intensité dépend fortement de la température mais est indépendant de la nature de l’émetteur.
- – le rayonnement thermique d’un corps chaud peut être absorbé par un corps froid mais PAS l’inverse.
1.2. Émission de rayonnement de fluorescence
En accord avec les principes de la mécanique quantique l’énergie interne d’atomes et molécules ne peut varier d’une manière continue. Les niveaux énergétiques sont discrets : on dit qu’ils sont « quantifiés ». Un atome ou une molécule peut être excitée d’un niveau d’énergie bas à un niveau plus élevé par différents mécanismes dont l’absorption d’un rayonnement de longueur correspondant précisément à la différence d’énergie entre les niveaux concernés. Un atome ou une molécule excitée, toujours de durée de vie limitée, peut se désactiver par différents mécanismes dont l’émission d’un rayonnement de fluorescence. Il va sans dire que la loi du rayonnement de Kirchhoff ne s’applique PAS au rayonnement de fluorescence. Cette loi, spécifique des corps noirs, précise qu’à l’équilibre thermique leur absorptivité doit être égale à leur émissivité.
Les caractéristiques essentielles d’un rayonnement de fluorescence sont que :
- – le spectre d’émission est discontinu, constitué de raies ou de bandes. Son intensité ne dépend PAS de la température et la relation de Stefan-Boltzmann (1) n’est PAS d’application. Le spectre de fluorescence dépend fortement de la nature de l’atome ou de la molécule et peut même servir à l’identifier.
- – le rayonnement de fluorescence d’un corps froid peut être absorbé par un corps chaud sans violer le second principe de la thermodynamique car un rayonnement n’est PAS de la chaleur.
1.3. Absorption de rayonnement thermique
Le rayonnement thermique d’un corps noir, par exemple le Soleil, peut être absorbé par un autre corps noir plus froid comme la Terre mais l’inverse n’est PAS possible. Par contre, certaines longueurs d’onde du rayonnement thermique d’un corps noir peuvent être absorbées sélectivement par des molécules individuelles à n’importe quelle température si une transition vers un niveau d’énergie plus élevée est possible. C’est le cas, par exemple, pour le rayonnement thermique du Soleil. La fig. 2 montre qu’au sommet de l’atmosphère le rayonnement thermique du Soleil correspond assez bien à celui calculé par l’équation de Planck pour un corps noir à 5250 °C avec un maximum à 500 nm. Comme mentionné ci-dessus, 95 % de l’émission se situe dans le domaine de longueurs d’onde s’étendant de 250 nm à 2000 nm (2 µm). Au niveau de la mer l‘intensité du rayonnement est réduite de 20 % car unefraction est absorbée par les gaz atmosphériques (essentiellement par la vapeur d’eau)dans les longueurs d’onde de 800 à 3000 nm (de 0,8 à 3 µm, modes de vibration de H2O apparaissant sur la fig. 6).

Le même type de phénomène intervient si on considère la Terre comme un corps noir à 288 K (15° C). La loi de Wien prévoit que le rayonnement émis devrait présenter un maximum d’intensité à 10 µm et l’équation de Planck permet de calculer que 95 % du spectre d’émission sera compris entre 5 et 40 µm. Une fraction de ce rayonnement thermique peut être absorbée principalement par la vapeur d’eau et, dans une moindre mesure, par le CO2 (voir paragraphes 2.2 et 2.3 ci-dessous).
2. Absorption et émission de rayonnement par les gaz atmosphériques
2.1. Niveaux d’énergie
Dans l’atmosphère terrestre 78 % des molécules sont des molécules d’azote N2 et 21 % sont des molécules d’oxygène O2. Le troisième constituant par ordre d’abondance est l’argon Ar (environ 1 % des molécules). Les molécules de CO2 n’interviennent que pour environ 0,04 %. L’énergie totale de ces molécules est la somme de leur énergie de translation d’une part et de leurs énergies électronique, de vibration et de rotation d’autre part. L’énergie de translation n’est PAS quantifiée. Elle peut donc varier de manière continue dans une gamme de valeurs qui dépend de la température et qui obéit à la fonction de distribution des vitesses de Maxwell-Boltzmann (voir fig.3).
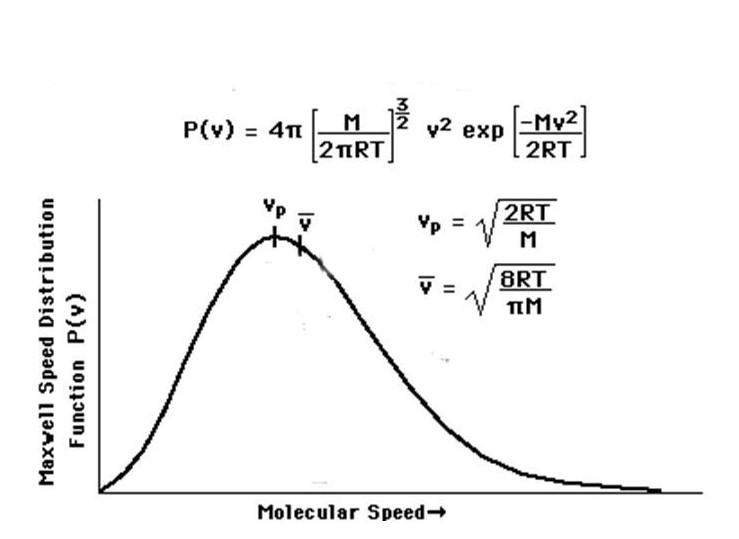
(Probabilité de trouver une molécule de vitesse V à une température T,
Vp = vitesse la plus probable,
V͞ = vitesse moyenne).
La théorie cinétique des gaz permet de calculer qu’à la température de 15°C les molécules de l’air sont animées de vitesses de l’ordre de 500 m par seconde et qu’à cette température et à la pression d’une atmosphère, chacune subit plusieurs milliards de collisions par seconde.
Les niveaux d’énergie électronique, de vibration et de rotation sont quantifiés. Les transitions entre niveaux électroniques se manifestent dans le domaine spectral de l’ultra-violet et du visible et nous n’en discuterons pas ici. En plus des mouvements de translation, toutes les molécules polyatomiques, si elles disposent de l’énergie suffisante, peuvent aussi entrer en vibration avec variation rapide et périodique des longueurs ou des angles de leurs liaisons interatomiques. Cependant, certaines transitions seulement entre niveaux de vibration apparaissent dans l’infrarouge car, pour qu’un mouvement de vibration s’y manifeste (en émission ou absorption) il faut que la vibration implique une variation de moment dipolaire. C’est le cas pour certains modes de vibration de CO2 et H2O mais PAS pour N2 et O2 (ce qui ne les empêche pas de vibrer même si il n’y a pas de variation de moment dipolaire). Pour qu’un mouvement de rotation pure se manifeste (en émission ou absorption) dans l’infrarouge il faut que la molécule possède un moment dipolaire permanent. C’est le cas pour H2O mais PAS pour CO2, N2 ou O2 (ce qui ne les empêche pas d’avoir des mouvements de rotation même si elles n’ont pas de moment dipolaire permanent). Néanmoins, lors d’une vibration, des molécules comme CO2 et H2O peuvent se trouver dans différents états (sous-niveaux) de rotation. Des mouvements de rotation sont alors associés aux mouvements de vibration et les spectres sont qualifiés de spectres de vibration-rotation. Nous ne nous intéresserons ici qu’au CO2 et à la vapeur d’eau car ce sont les principaux gaz atmosphériques susceptibles d’absorber une fraction des rayonnements thermiques du Soleil ainsi que de la Terre.
2.2. Le CO2
Les molécules de CO2 possèdent trois modes de vibrations distincts notés :
- ν1 (étirement symétrique) à 7,5 µm,
- ν2 (déformation angulaire) à 15 µm
- ν3 (étirement asymétrique) à 4,3 µm
Les deux derniers sont actifs dans l’infrarouge mais seul ν2 se situe dans le domaine du rayonnement thermique de la Terre (de 5 à 40 µm). La fig. 4 met en évidence, en plus des niveaux de vibration correspondant à la transition ν2, la présence de sous-niveaux de rotation caractérisés par diverses valeurs du nombre quantique J. Les transitions possibles d’après la mécanique quantique correspondent à des transitions entre niveaux de rotation telles Δ J = – 1, Δ J = 0 et Δ J = + 1.
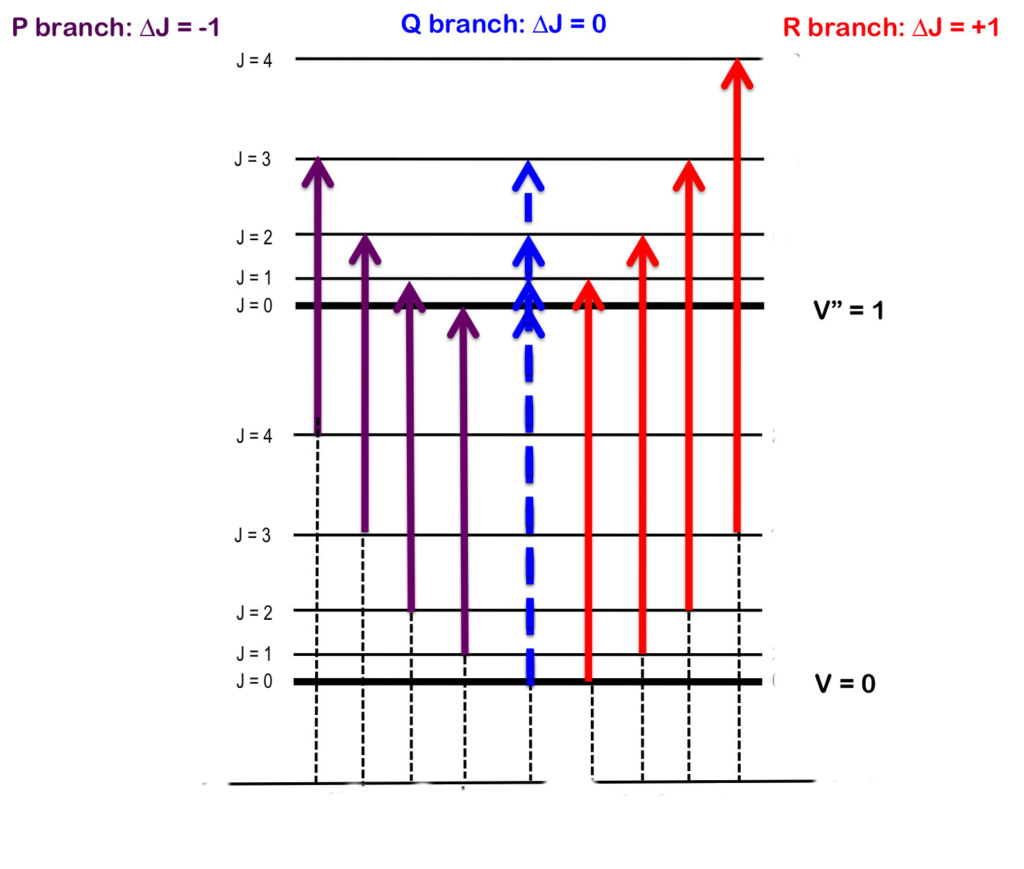
et transitions entre sous-niveaux de rotation
conduisant aux branches P, Q et R
du spectre infrarouge présenté sur la fig. 5.
La combinaison de toutes les transitions possibles se manifeste dans le spectre de vibration-rotation, reproduit à faible résolution sur la fig.5, par l’apparition de branches P, Q et R par ordre d’énergie croissante.
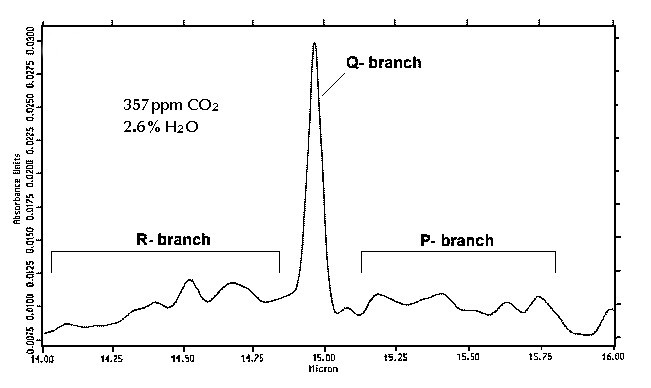
En admettant que la Terre se comporte comme un corps noir à la température de 288 K (15 ° C) et en intégrant l’équation de Planck dans le domaine d’absorption du CO2 de 14 à 16 µm (voir fig. 5) on trouve que 10 % seulement de l’énergie du rayonnement thermique de la Terre est émis dans cet intervalle de longueurs d’onde. Le CO2, quelle que soit son abondance, ne pourrait donc absorber plus que cette fraction.
2.3. La vapeur d’eau
De tous les gaz atmosphériques susceptibles d’absorber une fraction du rayonnement thermique de la Terre la vapeur d’eau est le plus efficace parce que c’est le plus abondant (en moyenne 2 % en volume) et aussi parce que son spectre infrarouge est le plus étendu. Les molécules d’eau possèdent trois modes de vibration notés :
- ν1 (étirement symétrique) à 2,7 µm,
- ν2 (déformation angulaire) à 6,3 µm
- ν3 (étirement asymétrique) à 2,7 µm
Les deux derniers seulement sont actifs dans l’infrarouge mais seul ν2 se situe dans le domaine du rayonnement thermique de la Terre (de 5 à 40 µm). Des combinaisons de ν1, ν2 et ν3 peuvent aussi être actives dans l’infrarouge comme le montre la fig. 6 (courbe verte). Elles sont hors du rayonnement thermique de la Terre mais PAS hors du rayonnement thermique du Soleil au sommet de l’atmosphère dont elles absorbent une fraction (voir fig.2). En admettant que la Terre se comporte comme un corps noir à la température de 288 K (15 ° C) l’intégration de l’équation de Planck de 5 à 8 µm, domaine de la large bande de vibration-rotation ν2 (fig.6) permet de calculer que 12 % de l’énergie du rayonnement thermique de la Terre pourraient être absorbés par la vapeur d’eau dans cet intervalle de longueurs d’onde. A cela s’ajoute l’absorption associée à la rotation pure des molécules d’eau qui, cas particulier parmi les gaz atmosphériques, possèdent un moment dipolaire permanent. Les transitions entre niveaux de rotation pure, notées R sur la fig. 6, s’étendent de 20 µm à 300 µm et même au-delà (en dehors de l’échelle du graphique). L’intégration de l’équation de Planck dans le domaine de 20 à 300 µm permet de calculer que 48 % de l’énergie du rayonnement thermique de la Terre pourraient être absorbés par la vapeur d’eau dans cet intervalle de longueurs d’onde. Au total, la vapeur d’eau pourrait absorber 60 % du rayonnement thermique de la Terre et, s’ajoutant aux 10 % du CO2(voir 2.2 ci-dessus) il ne resterait au rayonnement thermique de la Terre qu’une zone de transparence (fenêtre optique) de 8 à 13 µm (voir fig.10) permettant le passage de 30 % environ de ce rayonnement. Cette dernière valeur est confirmée en intégrant l’équation de Planck dans ce domaine de longueurs d’onde. Toutes ces valeurs seront utilisées pour établir le bilan énergétique de la Terre (voir paragraphe 4 ci-dessous).

à l’état solide (bleu),
liquide (rouge)
et gazeux (vert).
2.4. Vibration et rotation de CO2 et H2O dans les basses couches atmosphériques
L’importance des mouvements de translation des molécules atmosphériques dépend de la température comme indiqué plus haut (fig. 3). Il en est de même pour leurs mouvements de vibration et de rotation. Toutes ces molécules peuvent subir, à des degrés divers, des mouvements de vibration et de rotation si elles disposent de l’énergie suffisante. En l’absence de rayonnement extérieur, par exemple dans une boîte opaque, cette énergie provient du milieu ambiant sous l’action des nombreuses collisions qui sont un moyen d’échange énergétique. On peut calculer grâce à la relation Ev = hc/λ (où h est la constante de Planck, c la vitesse de la lumière et λ la longueur d’onde du rayonnement absorbé) les énergies requises pour provoquer les transitions de vibration de CO2 à 15 µm et de H20 à 6,3 µm ainsi que de rotation de H20 entre 20 et 300 µm. D’autre part, on peut calculer par la relation Et = mv2/2 quelles devraient être les vitesses des molécules N2 à 15° C pour atteindre ces énergies c’est-à-dire pour que Et = Ev. On trouve respectivement environ 700 m/s pour exciter la vibration de CO2 et 1100 m/s pour exciter la vibration de H2O. L’intégration de la fonction de distribution des vitesses de Maxwell-Boltzmann (fig. 3) montre qu’à 15 °C 20 % des molécules N2 ont une vitesse supérieure à 700 m/s et 1 % une vitesse supérieure à 1100 m/s. En fonction du principe d’équipartition des énergies on en déduit qu’à 15° C statistiquement 20 % des molécules CO2 seraient en état de vibration mais seulement 1 % des molécules H2O. Par contre, pratiquement toutes les molécules H20 seraient en état de rotation. Ce passage des molécules CO2 et H2O à leur plus bas niveau de vibration résulte seulement des collisions inélastiques (sans conservation de l’énergie cinétique) qui ne représentent que 0,001 % des collisions mais encore plusieurs dizaines de milliers par seconde. Dans ces conditions il y a conversion d’une fraction ∆ de l’énergie cinétique de translation des molécules N2 (ou O2) en énergie de vibration des molécules CO2 ou H2O
∆Ec (translation) de N2 + CO2 (ou H20) ↔ ∆Ev (vibration de CO2 ou H20) + N2 (4)
Cette conversion est réversible et les molécules se désactivent endéans quelques millisecondes pour retourner à l’état fondamental lors de nouveaux chocs avec les molécules environnantes. Il existe donc un équilibre dynamique résultant des très nombreuses collisions. Il ne dépend que de la température et de la pression (par le biais de la distribution des énergies et du nombre de chocs entre molécules). Quoique ce ne soient pas toujours les mêmes molécules qui sont en état de vibration la proportion de molécules CO2 ou H2O dans ces états reste constante à une température et une pression déterminées. Cet équilibre ne sera PAS modifié si, en plus, certaines molécules sont excitées par absorption d’une fraction du rayonnement infrarouge émis par la Terre. Dans ces conditions, les molécules excitées supplémentaires de CO2 et H2O joueront, en se désactivant par collisions, le rôle de convertisseur de ce rayonnement absorbé en énergie de translation des molécules environnantes principalement N2 et O2.
3. Effet de serre radiatif
La théorie du réchauffement climatique d’origine anthropique est basée sur une seule et fragile hypothèse : l’existence d’un effet de serre qui n’a jamais été mis en évidence expérimentalement. Il existe un grand nombre de définitions parfois fantaisistes de l’effet de serre. Dans un article paru en 2009(1) G.Gerlich et R.D.Tscheuschner en relèvent 14 différentes provenant de sources aussi variées que l’Organisation Météorologique Mondiale ou l’Encyclopedia Britannica. La plupart de ces définitions résultent d’une mauvaise compréhension du phénomène qui intervient réellement dans une serre agricole mais souvent aussi d’une méconnaissance des lois fondamentales de la physique.
Plus récemment M. Hertzberg, A. Siddons et H. Schreuder(2) ont examiné six définitions parmi les plus souvent citées et démontré qu’aucune ne résiste à un examen scientifique critique. Sans revenir sur ces énumérations mentionnons seulement l’affirmation de certains climatologues selon laquelle une preuve, si pas une définition, de l’effet de serre serait qu’en l’absence de gaz dits « à effet de serre » la température « moyenne globale » de la Terre ne serait pas + 15° C mais – 18° C. Cette dernière température (parfois qualifiée de température « effective ») est calculée en appliquant la formule de Stefan-Boltzmann (voir 1.1 ci-dessus) au flux énergétique moyen de 240 W m-2 mesuré par satellites à 800 km d’altitude. Ce type de calcul n’aurait de sens que pour une Terre sans atmosphère car la formule de Stefan-Boltzmann ne peut s’appliquer qu’en l’absence d’autres mécanismes de dissipation de l’énergie que le rayonnement thermique (voir http://www.science-climat-energie.be/2018/04/26/du-bon-usage-de-la-formule-de-stefan-boltzmann/ [ou ici]). Ce calcul serait quand même erroné car, en l’absence d’atmosphère, une partie de l’énergie reçue du Soleil ne serait pas réfléchie par les nuages. Les satellites devraient alors mesurer un flux supérieur à 240 W m-2. La différence, souvent mentionnée, de 33° C entre +15 °C et – 18° C n’a donc aucun sens physique et ne peut PAS être considérée comme la manifestation d’un effet de serre. La température de –18° C, mesurée à une altitude de 5100 m environ, n’a aucun intérêt particulier et résulte simplement de l’existence d’un gradient thermique dans l’atmosphère. Ajoutons encore que l’introduction dans des modèles informatiques de rétroactions positives ou négatives a permis de qualifier le réchauffement climatique de changement climatique car l’introduction de paramètres supplémentaires dans les modèles informatiques permet de justifier n’importe quelle variation du climat (voir http://www.science-climat-energie.be/2018/04/10/forcage-radiatif-sensibilite-climatique-et-retroactions-positives/ [ou ici]). Finalement les médias ont contribué à la propagation de l’expression plus alarmante encore de dérèglement climatique laissant entendre que le climat aurait toujours été prévisible avant qu’il ne soit perturbé par l’action de l’homme.
La seule définition de l’effet de serre décrivant clairement le phénomène envisagé par le GIEC (IPCC 2012, Glossary of terms) et répondant, de plus, au critère de réfutabilité énoncé par l’épistémologue Karl Popper est la suivante :
« L’effet de serre est un phénomène radiatif causé par des gaz tels la vapeur d’eau ou le CO2 qui absorbent une fraction du rayonnement infrarouge émis par la Terre et le réémettent ensuite dans toutes les directions et notamment vers la surface terrestre dont la température serait, de ce fait, plus élevée qu’en l’absence de gaz absorbant l’infrarouge. Ces gaz sont dès lors qualifiés de gaz « à effet de serre ».
Sans reprendre en détails les arguments déjà présentés pour réfuter l’hypothèse de l’effet de serre radiatif (voir paragraphe 2.4 ci-dessus et http://www.science-climat-energie.be/2019/02/14/le-rechauffement-climatique-dorigine-anthropique/ [ou ici]) nous rappellerons simplement que dans les basses couches atmosphériques le CO2 ayant absorbé une fraction du rayonnement thermique de la Terre se désactive par collisions (plusieurs milliards par seconde) avec les molécules environnantes et PAS par émission d’un rayonnement de fluorescence. On peut en conclure que l’effet de serre radiatif n’existe PAS et que les rétroactions imaginées pour amplifier son effet n’ont aucune justification. La désactivation radiative du CO2 ne peut être observée qu’à des altitudes de l’ordre de 80 – 100 km lorsque la pression atmosphérique est suffisamment faible pour que le nombre de collisions soit réduit à environ 1000/s. Le rayonnement émis dans toutes les directions à cette distance de la surface terrestre ne peut évidemment avoir d’influence sur la température de la Terre ou des basses couches atmosphériques.
4. Le bilan énergétique de la Terre
Le bilan énergétique envisagé est celui du système Terre-atmosphère et pas celui du globe terrestre isolé. Il est basé sur l’idée que pour maintenir une température constante la Terre (donc le système Terre-atmosphère) doit dissiper par différents mécanismes l’énergie reçue du Soleil : évaporation de l’eau des océans, convection de l’air et rayonnement thermique. De nombreux auteurs ont traité ce sujet mais certains font intervenir un phénomène de «back radiation» associé à un hypothétique effet de serre qui n’existe PAS et leurs conclusions sont dès lors contestables. Nous essayerons ci-dessous d’établir un bilan critique en distinguant ce qui peut être mesuré ou calculé et ce qui résulte seulement d’estimations ou d’hypothèses.
4.1. Énergie absorbée par la Terre
Au niveau de l’orbite terrestre chaque mètre carré placé perpendiculairement au rayonnement solaire reçoit, en moyenne sur l’année, une puissance de 1368 W. La valeur de 342 W m-2 au sommet de l’atmosphère est basée sur l’idée que chaque mètre carré de la surface terrestre reçoit en continu le quart de 1368 W car la Terre n’intercepte le rayonnement solaire que sur une surface égale à celle d’un disque de même rayon. Cette valeur n’est PAS mesurée mais estimée en admettant une distribution uniforme de l’énergie sur toute la surface terrestre sans tenir compte d’une variation en fonction de la latitude. En réalité la distribution de l’énergie est loin d’être uniforme comme le montrent les valeurs mesurées par les satellites CERES (Cloud and Earth Radiant Energy System) à des altitudes de l’ordre de 800 km. Elles varient entre 20 et 440 W m-2 en fonction de la latitude (fig.7 en haut). La valeur de 342 W m-2 mesurée aux environs des latitudes 37°N et 37°S est généralement acceptée comme valeur moyenne pour des raisons explicitées au paragraphe suivant.
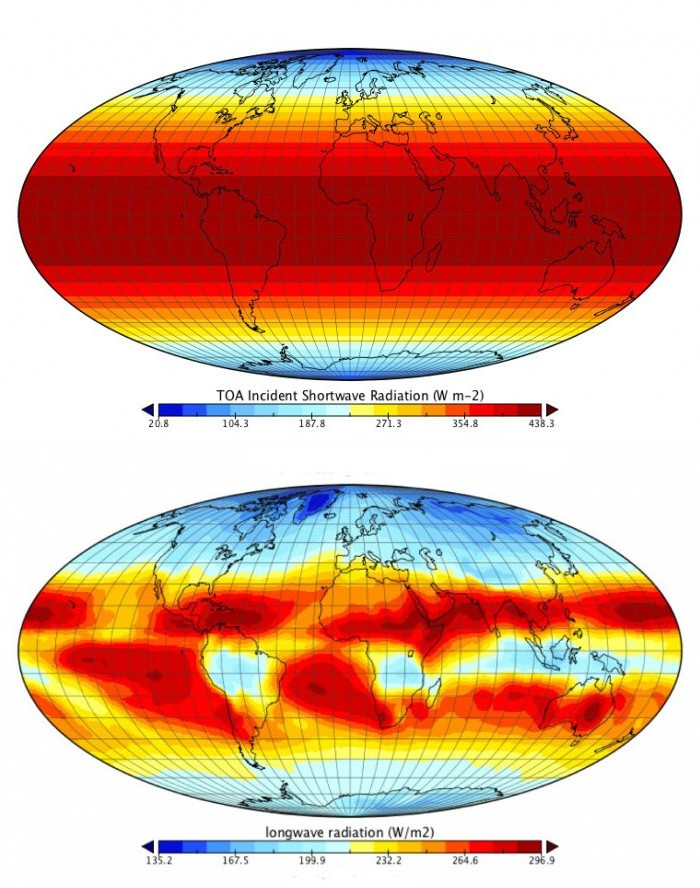
(mesurée par satellites CERES).
En bas : énergie émise par la Terre sous forme de rayonnement infrarouge
(mesurée par satellites ERBE).
La bonne compréhension de la discussion qui suit implique d’examiner simultanément la fig. 8 qui en résume les conclusions.
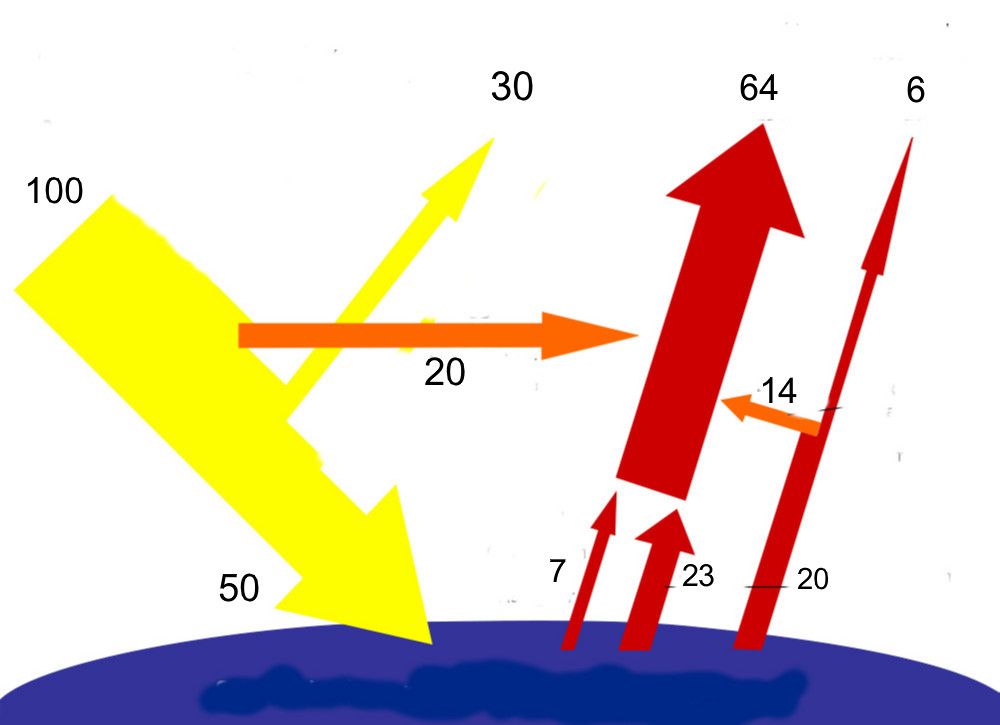
(énergie solaire au sommet de l’atmosphère 100 = 342 W m-2).
En attribuant à la Terre un albédo moyen de 0,3 impliquant 30 % d’énergie réfléchie ou diffusée par la surface terrestre, l’atmosphère et les nuages (valeur mentionnée sur la fig.8 et flèche jaune ascendante) le rayonnement effectivement absorbé par le système Terre-atmosphère serait alors réduit à 70 % de 342 W m-2, soit 240 W m-2. L’atmosphère (principalement la vapeur d’eau) absorberait 20 % de 342 W m-2 (voir fig. 2 ci-dessus et grande flèche orange sur la fig. 8). Finalement n’arriveraient à la surface terrestre que 50 % de 342 W m-2 (large flèche jaune descendante sur la fig. 8)
4.2. Énergie dissipée par la surface terrestre
Au niveau de la surface terrestre trois mécanismes permettent la dissipation de l’énergie reçue du Soleil : évaporation de l’eau des océans, convection de l’air et rayonnement thermique. Je remercie un lecteur d’une de mes précédentes notes d’avoir attiré mon attention sur le fait que la Terre reçoit chaque année sous forme de précipitations 5,05 105 km3 d’eau qui se répartissent sur la surface totale de 5,1 108 km2. Tenant compte de la chaleur de vaporisation de l’eau (2454 kJ/kg) et du nombre de secondes dans une année on peut calculer que 78 W m-2 seraient requis en continu pour évaporer cette quantité d’eau, ce qui représente environ 23 % de l’énergie reçue par la Terre au sommet de l’atmosphère (valeur notée sur la fig. 8).
La convection ascendante est généralement estimée à 7 % de l’énergie reçue au sommet de l’atmosphère (valeur notée sur la fig. 8). Le couplage de la convection et de l’évaporation de l’eau des océans constituerait donc, à raison de 30 %, le principal mécanisme de dissipation de l’énergie absorbée par la surface terrestre. Ces 7 % ne sont qu’une estimation mais, si on accepte cette valeur, on en déduit qu’environ 20 % de l’énergie reçue au sommet de l’atmosphère, resteraient à éliminer par rayonnement thermique (valeur notée sur la fig. 8). On peut calculer (voir 2.3) que 30 % de ce rayonnement pourraient être éliminés directement via la fenêtre optique (30 % de 20 % = 6 % de l’énergie reçue au sommet de l’atmosphère, mince flèche rouge en haut à droite sur la fig. 8) mais le reste serait absorbé principalement par la vapeur d’eau (à raison de 60 % voir 2.3) et aussi par le CO2 (à raison de 10 % voir 2.2) totalisant ainsi 70 % de 20 % et donc environ 14 % de l’énergie reçue au sommet de l’atmosphère (petite flèche orange à droite sur la fig. 8). L’ensemble de tous les pourcentages mentionnés en caractères gras ci-dessus est présenté sur la fig. 8.
Des mesures du rayonnement infrarouge émis par la Terre effectuées par les satellites ERBE (Earth Radiation Budget Experiments) à des altitudes de l’ordre de 800 km s’échelonnent entre 135 et 300 W m-2 selon la latitude (fig.7 en bas) et la valeur de 240 W m-2 est mesurée aux environs des latitudes 37°N et 37°S. La comparaison des deux cartes reproduites sur la fig. 7 est intéressante car elle indique que :
- Fig.7 en haut : aux latitudes de 37 °N et 37 °S la Terre reçoit du Soleil au sommet de l’atmosphère 342 W m-2 (mesurés par les satellites CERES) mais l’albédo en réfléchit 30 % (fig. 8) et donc seulement 240 W m-2 sont absorbés au niveau de la surface terrestre.
- Fig.7 en bas : aux latitudes de 37 °N et 37 °S la Terre émet sous forme de rayonnement infrarouge 240 W m-2 (mesurés par les satellites ERBE).
Au niveau des latitudes 37 °N et 37 °S il y aurait donc équilibre entre les flux radiatifs entrant et sortant du système Terre-atmosphère. Cela est explicité schématiquement sur la fig. 8 bis. Pour cette raison la valeur de 240 W m-2 mesurée à ces latitudes est généralement acceptée comme valeur moyenne des flux radiatifs entrant et sortant. Dans les régions proches de l’équateur la Terre reçoit du Soleil un excédent d’énergie par rapport à cette moyenne et dans les régions proches des pôles l’apport d’énergie est déficitaire par rapport à cette moyenne (fig.7 en haut). Lors de la dissipation radiative de l’énergie absorbée par la Terre, l’émission n’est PAS uniforme (fig.7 en bas) mais le déséquilibre est partiellement compensé par les transferts de chaleur dus au courants marins et aériens (fig.8bis). La correspondance des 240 W m-2 mesurés par les satellites ERBE avec l’énergie absorbée par le système Terre-atmosphère (70 % de 342 W m-2 = 240 W m-2)implique que, quel que soit le mécanisme initial de dissipation, l’énergie est finalement évacuée vers l’espace sous forme de rayonnement (large et mince flèches rouges en haut de la fig. 8).
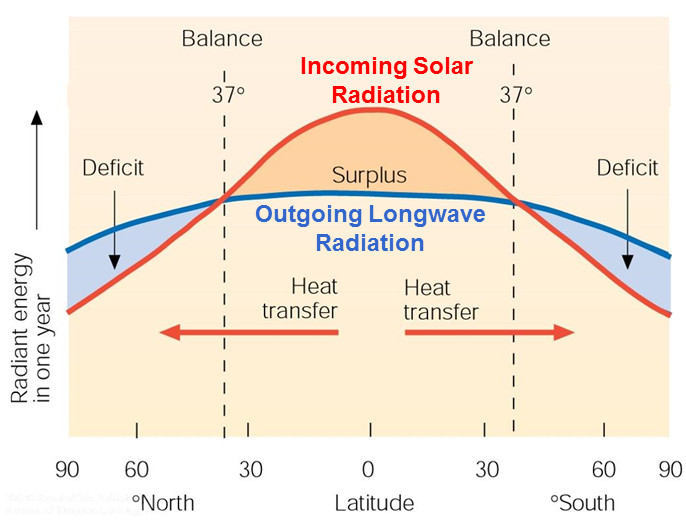
Ce bilan global est basé sur le modèle d’un système Terre-atmosphère en équilibre radiatif constant (sans accumulation ou libération temporaires d’énergie). Peu de grandeurs ont été réellement mesurées mais l’ensemble est cohérent et compatible avec les calculs rappelés dans les paragraphes 2.2 et 2.3. Son principal mérite est de mettre en évidence l’importance de la vapeur d’eau dans l’absorption d’une fraction des rayonnements thermiques du Soleil et de la Terre (flèches orange sur la fig. 8). Par voie de conséquence, la vapeur d’eau doit donc aussi avoir un rôle important dans la dissipation de cette énergie. Or, le bilan présenté ci-dessus n’apporte pas de réponse au problème posé par la conversion finale en rayonnement de l’énergie dissipée initialement par différents mécanismes (large flèche rouge ascendante sur la fig. 8). C’est à ce dernier aspect qu’est consacré le paragraphe suivant.
4.3. Origine du rayonnement détecté par satellites
Les principales sources d’information dont nous disposons proviennent des satellites NIMBUS 3 (1) et NIMBUS 4 (2). Mis en orbite à une altitude de l’ordre de 1100 km, ils étaient équipés d’un interféromètre IRIS (InfraRed Interferometer Spectrometer) permettant d’enregistrer les spectres infrarouges par transformée de Fourier. Un exemple de spectre enregistré par NIMBUS 4 près de l’équateur au dessus de l’océan Pacifique occidental est reproduit sur la fig.9.

La totalité de ce spectre ne peut PAS provenir directement de la surface terrestre car seule la fenêtre optique de 8 à 13 µm permettrait au rayonnement thermique d’être évacué vers l’espace sans être absorbé dans les basses couches atmosphériques (principalement par la vapeur d’eau). Cela apparaît clairement sur la fig.10 qui superpose au spectre de transmission (inverse de l’absorption) des basses couches atmosphériques la courbe d’émission (en rouge) d’un corps noir à 288 K (15° C) comme le serait la Terre.
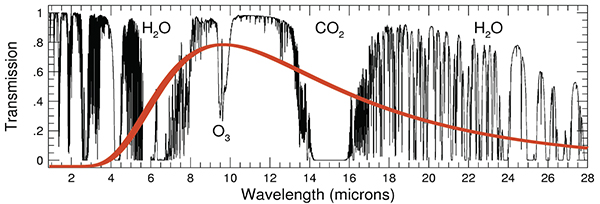
(fenêtre optique de 8 à 13 µm)
et spectre d’émission d’un corps noir à 288 K (15° C) (en rouge).
Sur la fig.9 apparaissent aussi en traits discontinus des courbes correspondant au rayonnement d’un corps noir aux températures mentionnées. Il semble qu’il y ait une tentative de faire correspondre chaque partie du spectre expérimental à une courbe d’émission « théorique » censée préciser la température à laquelle elle aurait été émise si elle provenait d’un corps noir. Cela pourrait éventuellement se justifier pour la partie du spectre de 8 à 13 µm si ce rayonnement provenait exclusivement de la surface terrestre à la température de 288 K (15° C) ce qui ne semble PAS le cas (voir ci-dessous). Pour le reste de la courbe expérimentale une telle hypothèse est injustifiée car aucun constituant atmosphérique, quelle que soit l’altitude d’où proviendrait le rayonnement, ne peut être assimilé à un corps noir dont l’intensité d’émission varierait en T4 (voir paragraphe 1 : deux types de rayonnement à ne pas confondre).
L’aire sous chaque partie du spectre de la fig.9 est proportionnelle au flux énergétique mesuré dans le domaine de longueur d’onde considéré. La portion la plus importante du spectre s’étend de 8 à 13 µm (correspondant à la fenêtre optique) mais elle n’a PAS l’allure attendue pour le rayonnement thermique de la Terre qui devrait présenter un maximum à 10 µm comme la courbe rouge de la fig. 10. De plus, la fig. 8 montre (fine flèche rouge à droite) que le rayonnement provenant directement de la surface terrestre à travers cette fenêtre optique ne représente que 6 % de l’énergie reçue par la Terre au sommet de l’atmosphère soit 21 W m-2. On peut en déduire que les satellites NIMBUS ont enregistré plus de rayonnement que celui provenant directement de la surface terrestre mais beaucoup moins que les 240 W m-2 mesurés par les satellites ERBE (fig.7 en bas). La majeure partie du rayonnement pris en compte dans ces 240 W m-2 n’apparaît donc PAS sur le spectre de la fig. 9 car hors du domaine de mesure de l’appareillage utilisé. L’ozone, dont la concentration est la plus élevée vers 30 km d’altitude, absorbe à 9,6 µm une fraction du rayonnement thermique provenant de la Terre avant qu’il n’atteigne les satellites, en accord avec la fig. 10. Quant au CO2 il absorbe entre 14 et 16 µm une fraction d’un rayonnement qui ne provient PAS directement de la surface terrestre et dont l’origine est discutée ci-dessous.
Quels constituants atmosphériques sont susceptibles d’apporter sous forme de rayonnement l’appoint énergétique pour atteindre les 240 W m-2 mesurés par les satellites ERBE ?
L’hypothèse la plus probable est que ce soit la vapeur d’eau car
- 1° de tous les constituants atmosphériques c’est le plus abondant de ceux qui sont susceptibles d’émettre un rayonnement infrarouge et c’est celui dont le spectre de vibration-rotation est le plus étendu (fig. 6).
- 2° de tous les constituants atmosphériques c’est le seul qui, dans la troposphère, peut s’y trouver sous les états solide, liquide et gazeux et donc y subir des changements d’état.
- 3° les parties du spectre de la fig. 9 situées de part et d’autre de la fenêtre optique soit de 6 à 8 µm d’une part et de 13 à 25 µm d’autre part correspondent précisément aux domaines d’absorption (et donc aussi d’émission) de la vapeur d’eau mentionnés sur la fig. 10. La fig. 6 permet de préciser que dans le premier cas il s’agit de transitions de vibration et dans le second de transitions de rotation.
Par quel mécanisme la vapeur d’eau pourrait-elle évacuer sous forme de rayonnement l’énergie absorbée par le système Terre-atmosphère ?
Les molécules H2O de l’atmosphère, excitées par absorption d’une fraction de l’énergie provenant du Soleil et de la surface terrestre (flèches orange sur la fig.8), ne peuvent PAS émettre de fluorescence, à quelque niveau que ce soit, car même à 12 km d’altitude, quand la vapeur d’eau est entièrement condensée (température et pression de l’ordre de – 60 °C et 200 hPa), la fréquence des collisions entre molécules (proportionnelle à P.T –1/2 ) n’est réduite que d’un facteur 4 par rapport aux basses couches atmosphériques et est encore de l’ordre de 109/s. Quelle que soit l’altitude, les molécules H2O individuelles se désactivent donc toujours par collisions avec les molécules environnantes N2 et O2 mais lors d’un changement d’état impliquant un grand nombre de molécules voisines la situation pourrait être différente.
La vapeur d’eau, entrainée par convection, se refroidit progressivement en s’élevant et se transforme en gouttelettes liquides qui, en présence de germes, peuvent partiellement cristalliser vers 4 km d’altitude à –10 °C. Lors de ces changements d’état les chaleurs latentes de vaporisation et de fusion sont libérées et cédées au milieu ambiant par collisions avec les molécules environnantes. Par suite de ce transfert de chaleur la température de l’air humide est toujours supérieure à celle de l’air sec à une altitude donnée. Cependant, la troposphère n’étant PAS à l’équilibre thermodynamique à cause des courants de convection ascendants et descendants, l’eau peut rester partiellement à l’état surfondu (c’est-à-dire liquide) à –10 °C alors qu’à l’équilibre elle devrait être solide. La vapeur d’eau peut aussi rester sursaturée jusqu’à des altitudes voisines de 10 km et ne se condenser en cristaux qu’à des températures de l’ordre de – 50 °C. Les états de liquide surfondu et de vapeur sursaturée sont des états métastables qui peuvent revenir brusquement à des états liquide ou solide stables conformes au diagramme des phases.
Lors du brusque passage d’un état métastable à un état stable les interactions entre un grand nombre de molécules H2O voisines deviennent prépondérantes, réduisant automatiquement les collisions avec les molécules environnantes, empêchant la libération d’énergie sous forme de chaleur et favorisant la libération sous forme de rayonnement. La condensation de la vapeur d’eau sursaturée en solide permettrait la libération de la chaleur latente de sublimation (47 kJ/mol) sous forme de fluorescence vibrationnelle à λ = 6,3 µm par exemple (niveau d’énergie 19 kJ/mol) en n’impliquant la désactivation radiative que de quelques molécules d’eau (2,5 en moyenne). De la fluorescence rotationnelle pourrait aussi être émise de λ = 20 à 300 µm (niveaux d’énergie de 0,4 à 6 kJ/mol) mais un plus grand nombre de molécules d’eau devraient intervenir pour atteindre 47 kJ/mol.
Quelques auteurs ont étudié l’émission de rayonnement infrarouge lors d’un changement de phase au départ d’un état métastable. Ce phénomène a été qualifié de « infrared characteristic radiation » (IRCR). Dans une brève revue(6) il est précisé que les mesures à partir d’états métastables sont délicates et que la caractérisation précise du rayonnement émis est difficile. Référence est faite cependant à des chercheurs russes qui auraient décelé l’émission d’un rayonnement infrarouge de 4 à 8 µm lors de la condensation de vapeur d’eau sursaturée et d’un rayonnement de 28 à 40 µm lors de la cristallisation de gouttelettes d’eau à l’état surfondu. Ces domaines de longueurs d’onde correspondent respectivement aux transitions de vibration et de rotation des molécules H2O (fig. 6). D’autres auteurs(5) ont mis en doute la validité des mesures de 28 à 40 µm et n’ont enregistré, lors de la condensation de vapeur d’eau sursaturée, qu’une large émission s’étendant de 4 à 22 µm avec un maximum d’intensité à 13 µm qui coïncide avec celui de la fig. 9. En dehors des expériences de laboratoire l’émission IRCC provenant d’états métastables a aussi été mise en relation avec des phénomènes atmosphériques(7). L’émission d’un rayonnement infrarouge de 8 à 14 µm aurait été observée lors du contact de vapeur d’eau sursaturée, entraînée par un courant ascendant, avec la base de nuages cumulus à la température de –5 °C. Le satellite GOES 8 (Geostationary Operational Environmental Satellite) aurait aussi détecté au dessus des océans dans le canal de 6,7 µm l’émission de rayonnement infrarouge correspondant à la fluorescence vibrationnelle de l’eau. Par contraste des taches sombres apparaissent au dessus des zones arides. Signalons encore que l’émission d’un rayonnement infrarouge de longueur d’onde non précisée a été mise en évidence lors de la cristallisation d’une goutte d’eau observée sous microscope(8).
Dans quelles conditions la vapeur d’eau pourrait-elle émettre de la fluorescence lors d’un changement d’état ?
La discussion et les résultats des paragraphes précédents montrent que, lors d’un changement d’état, la première condition pour que la libération des chaleurs latentes de vaporisation et/ou de fusion soit possible sous forme de rayonnement est qu’interviennent des états métastables (vapeur d’eau sursaturée ou eau liquide à l’état surfondu). Encore faut-il que la concentration locale en vapeur d’eau soit suffisamment faible pour que le rayonnement émis ne soit pas réabsorbé par les molécules d’eau individuelles puis converti en chaleur par collisions avec les molécules environnantes N2 et O2. Cette deuxième condition suggère que le phénomène ne pourrait se produire qu’à des altitudes voisines de 10 km où la teneur en vapeur d’eau n’est plus que de 0.01 % (fig. 11). A ce niveau, au sommet de la troposphère, la convection ascendante de la vapeur d’eau sursaturée s’arrête puisque le gradient thermique s’annule. Comme il n’y a plus des gouttelettes d’eau à l’état métastable seule la condensation de la vapeur d’eau sursaturée en microcristaux de glace peut être envisagée. Ce phénomène, inverse de la sublimation, est parfois qualifié en anglais de « desublimation » mais le terme correct en français est « condensation ».

Ce changement d’état permettrait-il l’évacuation radiative de l’énergie provenant de la surface terrestre ?
Nous avons vu au paragraphe 4.2 et sur la fig. 8 que l’énergie absorbée par le système Terre-atmosphère ne peut être évacuée que sous forme de rayonnement : 6 % directement par le rayonnement thermique de la Terre (21 W m-2) et 64 % (219 W m-2) après conversion en rayonnement de l’énergie résultant initialement de tous les autres mécanismes. La condensation de vapeur d’eau sursaturée en microcristaux de glace entre 9 et 10 km d’altitude rend-elle cette conversion possible ? Un calcul simple pourrait nous en convaincre.
La dissipation en continu de 219 W m-2 par toute la surface du globe terrestre (dont la valeur est mentionnée au paragraphe 4.2) représente au total 1,12 1017 J/s. Envisageons ensuite une couche atmosphérique s’étendant de 9 à 10 km d’altitude autour du globe terrestre (température et pression moyennes 230 K et 275 hPa). L’équation des gaz parfait permet de calculer le nombre total de molécules qu’elle contient d’où le nombre de molécule H20 à l’état de vapeur sursaturée qui n’en représentent que 0,01 % soit 7,36 1014 mol. Lors de la condensation à l’état solide, ces molécules H2O pourraient dissiper sous forme de rayonnement 47 kJ/mol soit au total 3,46 1019 J. Cette énergie émise quasi instantanément sous forme de rayonnement est 310 fois supérieure à l’énergie à évacuer par seconde. Comparant les valeurs soulignées on voit que, même si le rendement de conversion en rayonnement n’était que de 0,3 %, il permettrait encore d’évacuer l’énergie dissipée chaque seconde par la surface terrestre.
Nous pouvons donc conclure que, sur les 240 W m-2 mesurés par les satellites ERBE, 9 % (21 W m-2) proviennent directement de la surface terrestre sous forme de rayonnement thermique et 91 % (219 W m-2) de l’émission de fluorescence associée à la condensation de la vapeur d’eau sursaturée au sommet de la troposphère.
Cette hypothèse nous permet de considérer la fig. 9 comme la superposition du rayonnement thermique de la Terre transmis directement à travers la fenêtre optique de 8 à 13 µm et d’un large spectre de fluorescence vibrationnelle et rotationnelle des molécules H2O qui pourrait s’étendre de 4 µm à plus de 100 µm (fig. 6) et donc bien au-delà des 25 µm qui constituent la limite de la fig.9. Cela explique pourquoi les 240 W m-2 mesurés par satellites ERBE n’apparaissent que très partiellement sur la fig. 9. On comprend aussi qu’une fraction de la fluorescence rotationnelle puisse être absorbée par le CO2 entre 14 et 16 µm comme le montre la même figure.
Références
⚠ Les points de vue exprimés dans l’article ne sont pas nécessairement partagés par les (autres) auteurs et contributeurs du site Nouveau Monde.




















