Des mesures sans queue ni tête

[Source : ndt.net]
[Traduction John Hunter (révisée par J. S).]
Par Terry Oldberg et Ronald Christensen.
Publié initialement par l’American Society of Mechanical Engineers. 1995.
RÉSUMÉ
Cet article expose une incohérence dans le domaine du contrôle non destructif (CND) [de structures et de matériaux] et souligne les dangers de la confusion qui en découle. Les objets physiques présents dans une population statistique occupent une partition de l’ensemble des objets physiques considérés. Cependant, de nombreuses procédures de CND testent des objets physiques qui ne figurent pas dans une telle partition. L’incohérence a lieu lorsque les scientifiques CND représentent des objets physiques qui n’occupent pas de partitions comme éléments de populations dans leurs études sur la fiabilité du CND. Les populations fictives invalident la définition de la probabilité en tant que mesure d’un événement dont la valeur pour un cas certain est 1.
La probabilité étant invalidée en tant que mesure de la fiabilité d’un test, les scientifiques du CND ont procédé en représentant une mesure différente d’un événement sous la forme d’une « probabilité ». Le lecteur qui interprète la mesure de l’étude comme une probabilité se trompe donc sur plusieurs points. Par exemple, la certitude apparemment parfaite qui accompagne une valeur de 1 pour la probabilité de détection de l’étude est en fait une ambiguïté parfaite parce que la valeur de cette mesure sur l’événement certain d’un défaut est de 2. Des conséquences graves sont imaginables si un ingénieur de réacteur devait agir sur la base de la représentation de l’USNRC [U. S. Nuclear Regulatory Commission : Commission de réglementation nucléaire des États-Unis].
Les auteurs recommandent d’éviter les conséquences d’une telle confusion et d’autres cas de confusion en revisitant les rapports du passé d’après nos recommandations. Celles-ci emploient un langage qui permet de distinguer les probabilités et les populations correctes de celles qui ne le sont pas. À plus long terme, ils recommandent la refocalisation du CND sur des probabilités et des populations correctes.
Introduction
La probabilité est une mesure d’un événement dont la valeur pour un événement certain est 1. (Halmos, 1950) Cependant, certaines irrégularités dans la conception d’une population statistique d’une étude peuvent donner une probabilité dont la valeur pour un événement certain est susceptible de s’écarter significativement de 1. À l’instar d’un « yard » étalon qui s’écarterait sensiblement du 0,9144 mètre orthodoxe, cette « probabilité » a la capacité d’induire gravement les gens en erreur. Le fait qu’elle ait été la mesure insoupçonnée de la fiabilité du contrôle non destructif (CND) dans des domaines de l’ingénierie sensibles aux erreurs incite à formuler l’avertissement suivant.
Les ingénieurs utilisent le contrôle radiographique, le contrôle par ultrasons et d’autres méthodes de contrôle non destructif pour diagnostiquer des problèmes avec des structures qui fonctionnent sous un stress mécanique. Ils sont particulièrement enclins à l’utiliser dans des situations où la défaillance d’une structure pourrait causer des dommages. Cependant, le CND peut lui-même causer des dommages lorsqu’il est erroné. C’est pourquoi les ingénieurs ont été amenés à établir les probabilités d’erreur dans les différentes méthodes de CND. Ces « probabilités » n’en sont parfois pas.
Notre article comporte trois parties. La première, PROBABILITÉ versus PSEUDOPROBABILITE, établit et oppose deux mesures d’un événement. La probabilité est consistante avec la population. La pseudoprobabilité est consistante avec la pseudopopulation ou bien une population irrégulière. Ces deux mesures sont légitimes, mais différentes. Donc quand la littérature appelle « probabilité » la pseudoprobabilité d’une étude, il y a tromperie.
La seconde partie, UNE CONFUSION NUCLÉAIRE, expose ce type de confusion dans une étude de la Commission de réglementation nucléaire des États-Unis. En ce qui concerne les niveaux dangereux d’endommagement d’un composant de réacteur nucléaire, sa probabilité de détection est une pseudo-probabilité dont la valeur est de 2 pour l’événement certain d’un défaut. Donc la valeur de 1 que l’agence considère comme la probabilité de découvrir une condition dangereuse dans un réacteur suggère une certitude absolue que le test est valide, mais est en fait une ambiguïté parfaite quant à la validité du test.
La troisième partie, CONCLUSION ET RECOMMANDATIONS, avertit le lecteur de s’attendre à des surprises du même genre dans toute la littérature CND. La recommandation étant que la littérature soit transformée dans le langage des pseudoprobabilités et que cesse la confusion. Nous proposons que la littérature CND soit restructurée pour définir des populations réelles et des probabilités.
PROBABILITÉS contre PSEUDOPROBABILITÉS
Dans Sampling Techniques, le statisticien William Cochran propose une règle qui permet d’obtenir une population [statistique] lorsqu’elle est respectée. Avant de chercher un exemple d’étude, sa population doit être divisée en objets physiques qu’on nomme des unités. Ces unités doivent couvrir la population totale et ne doivent pas faire double emploi, dans le sens que chaque élément de la population appartient à une unité et une seule (Cochran 1977). Les unités d’une étude doivent occuper une partition de la population. Dans la suite de l’article, nous nous efforcerons d’expliquer ce que cela signifie.
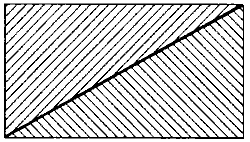
Une partition. La classe de deux triangles est une partition du rectangle.
On dit qu’une classe {A1, …, An} d’ensembles A1, …, An est une partition de l’ensemble A si chaque élément de A appartient à un ensemble dans {A1, …, An} et si deux ensembles dans {A1, …, An} n’ont pas d’élément en commun. La figure 1 montre une classe de deux triangles qui est une partition d’un rectangle. Dans cet exemple du diagramme de Venn, une classe est représentée par un ensemble d’objets géométriques, un ensemble par un objet géométrique seul et un élément de l’ensemble par un point à l’intérieur d’une limite d’un objet géométrique.
Nous allons référencer une classe {A1 …, An} comme une pseudopartition d’un ensemble A si cela n’est pas une partition de A. La figure 2 montre un exemple de pseudopartition. La classe de deux cercles est une pseudopartition du rectangle. Noter la région de superposition entre les deux cercles et la région du rectangle qui n’est pas couverte par un cercle.
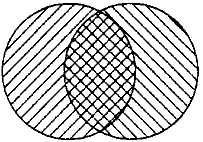
Une pseudopartition. La classe des deux cercles est une pseudopartition du rectangle.
Dans cet article l’entité que Cochran nomme « un élément dans la population » sera appelée un point de données. Dans l’étude du test de confiance, chaque point de données est une paire de nombres représentant les valeurs véritables et vérifiées de la propriété d’un objet physique et qui est mesurée par le test. L’ensemble complet des points de données possibles se nomme espace d’échantillonnage. Un événement est un sous-ensemble d’un espace d’échantillonnage.
Pour caractériser la fiabilité du test, son investigateur sélectionne une partition de l’espace d’échantillonnage. Puis il estime une valeur pour la probabilité de chaque événement dans la partition. Bien qu’il existe une grande variété de partitions, les chercheurs choisissent généralement la plus simple. Ses événements sont appelés un vrai positif, un faux négatif, un vrai négatif et un faux positif.
La figure 3 montre l’espace d’échantillonnage qui se rapporte à l’étude de la fiabilité des tests et cette partition de l’espace.
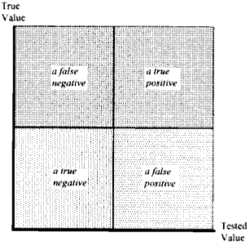
L’espace-échantillon qui se rapporte à l’étude de la fiabilité des tests et la partition la plus populaire de celle-ci.
La fréquence relative d’un événement est le nombre d’objets physiques qui participent à l’événement divisé par le nombre de points de données dans l’espace d’échantillonnage. La probabilité d’un événement modélise la fréquence relative du même événement. Inversement, la valeur de la fréquence relative d’un événement permet de vérifier empiriquement la valeur qu’une certaine théorie attribue à la probabilité de cet événement. La validation empirique est le sceau de la Science (K. Popper 1959).
De ce point de vue de la validation empirique, un événement certain a une signification particulière, car la valeur de sa probabilité est 1 selon sa définition. La fréquence relative d’un événement certain est le nombre d’objets physiques qui participent à l’événement divisé par le nombre de points de données dans l’événement. Par exemple, dans un test de patients pour le [supposé] virus de l’hépatite B, la fréquence relative d’un événement certain d’un vrai positif est le nombre de patients vrais positifs divisé par le nombre de résultats vrais positifs. Une fréquence relative d’un événement certain et dont la valeur est 1 cadre avec la définition de la probabilité. Une fréquence relative d’un événement certain dont la valeur n’est pas 1 ne cadre pas avec la définition de la probabilité.
La fréquence relative d’un événement certain est une mesure du degré de couverture de cet événement par des objets physiques. Quand la fréquence relative de chaque événement dans une partition d’un espace d’échantillonnage d’une étude est 1, cela signifie que chaque objet physique dans l’ensemble complet qu’ils forment participe dans un et un seul événement. Si cela est vrai, la classe des ensembles d’objets physiques qui participent aux événements variés est une partition de l’ensemble complet des objets physiques.
Il y a deux autres possibilités. Dans la première, il y a des objets physiques qui participent dans plus qu’un seul événement dans une partition d’un espace d’échantillonnage. Dans ce cas, on dit que les ensembles des objets physiques qui correspondent à ces événements se superposent. Dans la seconde, moins d’objets physiques participent dans un événement qu’il y a de point de données. On dit donc que l’ensemble des objets physiques correspondant à cet événement couvre imparfaitement l’événement. Si la classe d’ensembles d’objets physiques correspondant à la partition d’un espace d’échantillonnage présente une sous-couverture ou un chevauchement, il s’agit d’une pseudopartition de l’ensemble complet d’objets physiques. Ceci ne cadre pas avec le processus de vérification empirique d’un modèle de probabilité puisqu’une partition cadre avec le processus de vérification empirique. La vérifiabilité empirique étant la marque de fabrique de la science, la différenciation entre pseudopartition et partition revêt une grande importance scientifique.
Dans les statistiques normales, on appelle « unité » un objet physique qui appartient à une partition, « population » un ensemble d’unités et « sous-population » un sous-ensemble d’une population. Aucune terminologie uniforme n’est apparue dans le domaine des statistiques anormales, c’est pourquoi nous allons en inventer une. Un objet physique qui appartient à une pseudopartition est une « pseudo-unité ». Un ensemble de ces pseudo-unités, une « pseudopopulation » et un sous-ensemble de celles-ci, une « pseudo sous-population ». Pour compléter l’analogie, nous définissons la pseudoprobabilité comme une mesure d’un événement dont la valeur sur un événement certain est égale à la valeur de la fréquence relative de cet événement. La valeur de la pseudoprobabilité d’un événement certain est vérifiée empiriquement par la fréquence relative du même événement. Donc une pseudopartition d’un ensemble complet d’objets physiques cadre avec la vérifiabilité d’un modèle pseudoprobalistique.
Le physicien Lazar Mayant a noté que la discipline qui inclut le concept de probabilité, partition, population, subpopulation et unité est empiriquement vérifiable et donc peut être considéré comme Science (Mayant 1984). Selon lui, c’est la probabilistique. On peut noter que la discipline qui inclut les concepts de pseudoprobabilité, pseudopartition, pseudopopulation, pseudo sous-population et pseudo-unité est aussi empiriquement vérifiable et donc aussi une Science. Nous la nommerons pseudoprobalistique.
Bien que la probabilistique et la pseudoprobabilistique soient toutes deux cohérentes sur le plan interne, leurs concepts ne peuvent pas être mélangés. Il est donc important de séparer les deux concepts d’un point de vue linguistique. La confusion serait de mélanger pseudoprobabilité et probabilité. C’est arrivé avec l’USNCR (US nuclear commission regulation).
La confusion nucléaire
E.R Bradley et ses collègues étudièrent la fiabilité de CND dans des tubes de générateur à la vapeur d’un réacteur nucléaire (Bradley et coll. 1988). Les tubes contiennent l’eau qui refroidit le réacteur et transfèrent la chaleur à l’extérieur. Si les tubes se rompent, le cœur du réacteur concerné fond et la charge radioactive s’échappe dans la biosphère. Mais les tubes peuvent souffrir de corrosion. Un certain nombre de tubes a éclaté pendant l’opération et l’USNRC a depuis lors déclaré des inspections périodiques par CND.
L’étude de Bradley est la seule à compter. Elle est substantielle. L’inspecteur scanne à distance les tubes avec un senseur. Le senseur est inséré dans le tube qui doit passer l’inspection. Il parcourt le tube et émet des données. Celles-ci sont décodées par l’inspecteur. La procédure indique le dommage interne. Chaque indication contient une estimation de la pénétration radiale du tube par la corrosion, l’identité du tube et la position axiale du capteur. Les indications sont enregistrées.
Bradley demanda à l’équipe d’inspecteurs de tester un certain nombre de tubes selon la routine. Ces prescriptions émanent de la ASME (American society of Mechanical engineers) sous la direction de l’USNRC. Puis les tubes furent démontés pour tenter d’établir la fiabilité de leur inspection. En construisant le modèle de fiabilité, Bradley sélectionna la partition de l’espace d’échantillonnage, celle qui contient un vrai positif, un faux négatif, un vrai négatif et un faux positif.
En mécanique comme en statistique, vrai positif et faux négatif sont appelés des défauts. Dans le cas d’un événement vrai négatif ou faux positif, on parle de non-défauts. Les deux événements défaut et non-défaut forment une partition d’un espace d’échantillonnage dans l’étude de la fiabilité du test.
Une simplification se produit quand un défaut et un non-défaut sont certains. Avec le défaut certain, la probabilité ou la pseudoprobabilité d’un vrai positif et la pseudoprobabilité d’un faux négatif sont égales à la fréquence d’un événement certain d’un défaut. Comme probabilité et pseudoprobabilité sont dépendants, la fiabilité d’un texte peut être caractérisée par les termes d’une d’entre elles seulement. Bradley appuie cette caractérisation sur la probabilité ou la pseudoprobabilité d’un vrai positif. Il l’appelle probabilité de la détection.
Même chose avec un non-défaut certain. La probabilité ou pseudoprobabilité d’un vrai négatif et la probabilité ou pseudoprobabilité d’un faux positif sont égales à la fréquence relative d’un événement certain d’un non-défaut. Comme probabilité et pseudoprobabilité sont dépendantes, la fiabilité du test peut être caractérisée dans les termes d’une seule de ces deux catégories.
Quand on lit le rapport de Bradley, on note une incongruité dans l’utilisation de la terminologie, ce qui gêne la compréhension de la question : l’ensemble complet des objets physiques du test ASME/USNRC contient-il des unités ou des pseudo-unités ? Les objets physiques sont identifiés comme « défauts », mais un défaut est le nom d’un événement et pas un objet physique comme plusieurs statisticiens insistent auprès de leurs lecteurs (Bocker et coll. 1972. Juran 1974).
Cependant, pour Perdijon, dans un article récent écrit que dans le CND, le « défaut » désigne souvent un objet qui a une certaine limite dans l’espace. Il suggère que le terme « discontinuité » soit réservé à un objet de ce genre (Perdijon 1993). Dans certains cas, une discontinuité dans la limite entoure le matériau. Alors l’objet physique est défini par sa limite.
Cette conception du « défaut » peine à résoudre la question, car les « defauts » de Bradley sont presque en totalité les vides à l’extérieur du tube que la corrosion attaque. Un vide est une limite définie qui n’entoure aucun matériau et n’est pas physique. Un tel objet ne possède aucune propriété intrinsèque que le CND puisse mesurer.
S’ils n’ont pas de propriétés, alors les « défauts » de Bradley ne font rien pour appuyer l’établissement des valeurs de propriété dont il parle. On imagine que Bradley considère les discontinuités comme dictant les propriétés des objets physiques dans lesquels elles sont inscrites. Cependant notre conclusion est qu’il y a une différence minime entre ces objets physiques et ces discontinuités, si bien que Bradley balaye la distinction. Selon cette théorie, le « défaut » de Bradley est un territoire de discontinuité plus une fine couche de matériau qui adhère à son extérieur. Cette couche est assez mince pour que les dimensions d’un « défaut » soient essentiellement les mêmes que les dimensions de la discontinuité qui y sont enchâssées. Mais ce « défaut » est un objet physique à cause du matériau. Nous adopterons la théorie de Bradley quant au « défaut » en procédant à notre analyse de son étude tout en mettant entre guillemets le mot lui-même pour rappeler au lecteur qu’il désigne un objet physique et pas un événement. Quand le mot désigne un événement, il sera en italiques.
Les « défauts » de Bradley ont été définis par les métallurgistes qui pratiquent des tests de destruction après l’inspection des tubes. Les 108 « défauts » étaient courts, avec dans l’axe une longueur moyenne de 1 pouce. À ±3 pouces, l’incertitude positionnelle axiale de chaque indication était plutôt grande en comparaison. Donc chaque indication répertoriée comme « défaut » pouvait ne pas avoir enregistré ce « défaut ». De la même manière, chaque indication qui n’est pas un « défaut », mais ceci a 3 pouces près, aurait pu être rapportée comme « défaut ». En raison de la grande incertitude positionnelle, la question de savoir si une indication tombant à moins de 3 pouces de l’extrémité d’un « défaut » faisait référence à ce « défaut » ou n’y faisait pas référence avait une réponse totalement ambiguë.
Bradley a résolu ce problème de manière à faire écho au thème de cet article. Si le « défaut » a une indication à l’intérieur de 3 pouces, c’est un vrai positif. Sinon c’est un faux négatif. Ensuite, il a divisé le nombre de « défauts » qui sont vrai positifs par le nombre total de « défauts » et encapsulé le tout dans le ratio de la probabilité de détection. Bradley représente cette méthodologie dans un graphique (figure 4) avec pour ordonnée la probabilité de détection et pour abscisse la perte de la partie métallique. C’est le degré de pénétration de l’épaisseur du tube par un « défaut ».
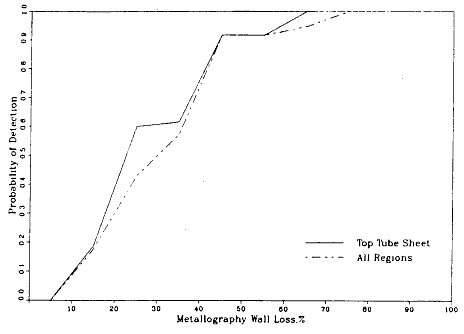
Graphique de la probabilité de détection en fonction de la perte métallurgique de paroi (Bradley et coll., 1988.)
La figure 4 montre que la probabilité de détection passe de 0, lorsque la perte métallurgique de la paroi est inférieure à 5 %, à 1, lorsque la perte métallurgique de la paroi est supérieure à 75 %. Comme les tubes sont hors service quand la perte de la partie métallique est plus de 80 %, ce graphique représente la certitude qu’un « défaut » sera signalé lorsqu’il atteindra un niveau de corrosion dangereux. Cependant, cette représentation est en contradiction avec notre observation précédente : il est totalement ambigu de savoir si une indication fait référence à un « défaut » particulier ou à quelque chose d’autre. Analysons comment ce conflit survient, dans le cadre de la probabilistique et de la pseudoprobabilistique.
La probabilité de Bradley estime les résultats sur la base d’une méthodologie dans laquelle il assigne un faux négatif à un « défaut » s’il ne l’assigne pas à un vrai positif. Cette méthodologie cadre avec l’assomption que le test ASME USNRC définit une partition de l’ensemble complet des objets physiques sous test. À cet effet Bradley suggère qu’une unité du matériel inspecté tombe toujours dans les catégories suivantes :
- *vrai positif si l’indication de défaut est rapportée et il y en a un en vérité.
- *faux positif si une indication de défaut est rapportée, mais il n’y en a aucun.
- *faux négatif : pas de rapport d’un défaut, mais il existe.
- *vrai négatif : pas de rapport de défauts et pas de défaut présent.
Ceci est une description de la partition.
Cependant la logique de Bradley implique un conflit avec cette assomption. Chaque « défaut » est vrai positif s’il est à l’intérieur de 3 pouces d’une indication. La même règle attribue aussi chaque « défaut » de ce type à un faux négatif. Examinons les conséquences de cette ambiguïté.
La probabilité de détection de Bradley (voyez la figure 4) est soit la probabilité d’un vrai positif, soit la pseudoprobabilité d’un vrai positif. Il s’agit d’une probabilité si la fréquence relative de l’événement certain d’un défaut est de 1 et d’une pseudoprobabilité dans le cas contraire. On désigne par ntp le nombre de « défauts » que Bradley attribue à un vrai positif et nfn le nombre qu’il attribue à un faux négatif. On désigne par fd la fréquence relative de l’événement certain d’un défaut.
Alors :
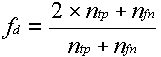 (1)
(1)
Nous avons doublé ici le nombre de « défauts » que Bradley attribue au vrai positif en calculant le nombre d’objets physiques qui correspondent à un vrai positif ou à un faux négatif parce que Bradley dans sa logique attribue un « defaut » à un faux négatif chaque fois qu’il en attribue un à un vrai positif, mais Bradley ne l’a pas attribué [directement] à un faux négatif. Bradley estime la probabilité de la détection dans la figure 4 à partir de :
Probabilité de détection = 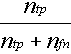 (2)
(2)
Si on combine les équations (1) et (2) on conclut que la fréquence relative d’un événement certain d’un défaut est donnée par :
Fd = 1 + probabilité de détection.
On voit que la valeur de la fréquence relative d’un événement certain d’un défaut va de 1 (quand la probabilité de détection est à sa valeur minimale de 0) à 2 (quand la probabilité de détection est à sa valeur maximale de 1). Quand la probabilité de détection est 0, c’est une probabilité. Quand la probabilité de détection a une valeur qui n’est pas 0, c’est une pseudoprobabilité.
La condition que la probabilité de détection ait une valeur de 1 est vraiment pertinente, car c’est sa valeur selon la figure 4 et à de dangereux niveaux de dommage. Sous cette condition, la probabilité de détection est une pseudoprobabilité avec valeur de 2 dans l’événement certain d’un défaut. Ainsi, la valeur de 1 pour la probabilité de détection à des niveaux de dommages dangereux doit être considérée comme 50 % de la valeur de la pseudoprobabilité de l’événement certain d’un défaut et non comme 100 % de la valeur de la probabilité de l’événement certain d’un défaut, comme l’implique le choix de langage de la figure 4.
50 % d’une pseudoprobabilité avec une valeur de 2 sur l’événement certain d’un défaut raconte une histoire différente que 100 % d’une probabilité. Et en particulier une valeur de 2 pour la pseudoprobabilité d’un événement certain d’un défaut indique une superposition complète des pseudopopulations qui correspondent à un vrai positif et à un faux négatif. La valeur de 1 pour la probabilité de détection à des niveaux dangereux de dommages n’indique rien d’autre que le fait que 50 % des pseudo-unités correspondant à un défaut sont attribuées par le test ASME-USNRC à un vrai positif. L’ambiguïté est totale. Ce test est-il valide pour diagnostiquer de dangereux niveaux de dommage ? Mais l’usage du langage certifie que le test est valide. Un ingénieur nucléaire qui prend l’ambiguïté de la figure 4 comme une certitude pourrait commettre une erreur désastreuse.
La partie restante de la méthodologie de Bradley concerne l’événement certain d’un non-défaut, c’est-à-dire un vrai négatif ou un faux positif. Bradley trouve qu’il y a de nombreuses indications sans « defauts » à l’intérieur de 3 pouces et les met dans le faux positif. Il n’attribue aucun objet à un vrai négatif. Il ne suggère aucune valeur pour une probabilité d’un faux positif ou un faux négatif, mais ceci n’a pas d’importance, car… « … la question de la sécurité liée à la fiabilité du CND ne dépend pas de la quantité de matériau non défectueux constatée, mais de l’identification du matériau défectueux ».
Analysons ceci du point de vue de la probabilité et de la pseudoprobabilité. Même si Bradley n’attribue aucune valeur à la probabilité ou la pseudoprobabilité d’un vrai négatif ou d’un faux positif, ses données fournissent la base pour établir des valeurs exactes pour elles. L’analyse qui conduit à ces résultats commence avec le calcul de la fréquence relative d’un événement certain d’un non-défaut.
L’attribution par Bradley de son nombre d’indications au-delà de 3 pouces d’un « défaut » à un faux positif signifie qu’il y a des points de données dénombrables dans une zone non-défaut. Alors qu’il y a des points de données, il n’y a pas d’objets physiques. La fréquence relative est toutefois donnée par le rapport entre les objets physiques et les points de données. Il s’ensuit que la valeur de la fréquence relative d’un événement certain d’un non-défaut est de 0.
Comme la valeur de cette fréquence relative n’est pas 1, toute mesure d’un sous-ensemble d’un non-défaut doit être une pseudoprobabilité et non une probabilité. Il s’en suit qu’un vrai négatif et un faux positif ont des pseudoprobabilités. La somme des valeurs de ces pseudoprobabilités est égale à 0.
On sait depuis la définition d’une mesure (Halmos 1950) que les 2 pseudoprobabilités ont des valeurs plus grandes que 0 ou égales à 0. Donc les pseudoprobabilités d’un vrai négatif et d’un faux positif ont une valeur de 0.
Si Bradley considère que l’absence de probabilité d’un vrai négatif ou d’un faux positif dans son rapport n’a pas d’importance dans une étude de sûreté, il exprime l’opinion selon laquelle il n’y a absolument aucun intérêt à maintenir en état de fonctionnement les équipements de production d’énergie nucléaire, car il est bien connu que la probabilité d’un vrai positif dans un test peut être améliorée arbitrairement, au prix d’une augmentation de la probabilité d’un faux positif [puisque la probabilité du vrai positif serait alors réduite]. On peut faire cela en produisant des indications dans des parties d’un tube de générateur à vapeur choisies au hasard. Une explication moins forte de cette absence serait que le test ASME USNRC ne cadre pas avec la définition de la probabilité.
Conclusions et recommandations.
Les irrégularités dans la pseudopopulation de Bradley peuvent être représentées dans le diagramme de Venn à la figure 2. Les deux cercles représentent les « défauts » qui correspondent à un défaut. Un de ces deux cercles représente ces « défauts » qui sont attribués à un vrai positif par le test ASME USNRC. L’autre cercle représente ces « défauts » qui sont attribués à un faux négatif par le test. L’aire du rectangle qui n’est pas couvert par un cercle représente l’événement d’un non-défaut. Il n’est pas couvert par des objets physiques. La région de superposition entre les deux cercles est nulle quand le niveau de dommage au tube qui envoie la vapeur est nul. Quand le niveau de dommage devient dangereux, les deux cercles se superposent complètement.
Les « defauts » du test ASME USNRC forment une « population » qui combine un manque de couverture totale et une superposition parfaite. Cependant cette population extrêmement irrégulière supporte les estimations des « probabilités » qui ont été publiées pour instruire les ingénieurs des réacteurs nucléaires par ASME USNRC !!!!! Cet incident nous incite à nous intéresser aux autres endroits où ce type de confusion peut se cacher.
Il y a des raisons de penser qu’il ne s’agit pas d’un cas isolé d’une population très irrégulière. Il y a un potentiel dangereux dans la définition de CND comme un champ qui détecte les « défauts » dans les matériaux. (Weissmantel 1975). Sommés d’établir la fiabilité de CND, les scientifiques ont fait en sorte que ces « défauts » occupent les populations de leurs études. Par exemple, les auteurs de « La fiabilité de l’inspection non destructive » ont simplement dit que les « défauts » occupent les populations (Silk et coll. 1987). D’autres ont eu une position équivalente : les irrégularités occupent les populations. Les directeurs de l’ASME et de l’USNRC sont d’accord (Beckjord 1991, Fernandez 1994). Un conseiller de l’USNRC sur la fiabilité de CND dans les réacteurs nucléaires (Bush 1991) opine pareillement. Il en va de même pour les auteurs d’une étude sur la fiabilité de la NDE dans un réacteur nucléaire britannique (Cartwright et coll., 1988). Toutefois, ces points de vue se sont révélés erronés en ce qui concerne le type de test qui attribue des « défauts » à des points de données en fonction de la proximité des « défauts » par rapport à des indications. C’est devenu une habitude maintenant pour les tests non destructifs des composants des réacteurs nucléaires. Le test ASME-USNRC des tubes de générateurs de vapeur nucléaires en est un exemple.
Chacun de ces tests attribue un « défaut » à un faux négatif quand il l’attribue aussi à un vrai positif ou bien n’attribue pas d’objet physique à un non-défaut. Le degré de sous-estimation d’un non-défaut peut être amoindri si on assouplit la loi de la preuve qui lie une indication au « défaut » avec la conséquence qu’on accroît le degré de superposition entre les ensembles des objets physiques qui correspondent à un vrai positif et à un faux négatif. Qu’il y ait sous-couverture, chevauchement ou les deux, les « populations » de ces « défauts » sont des pseudo-populations.
Les architectes de ces tests ont peut-être répondu aux besoins d’établir la fiabilité du CND en abandonnant ces tests ou en écrivant les rapports des études de fiabilité dans le langage des pseudoprobabilités. Mais cette réponse-là est bancale. Ils ont mixé la probabilistique avec la pseudoprobabilistique.
Le résultat de cette confusion peut être dangereusement trompeur. C’est pourquoi nous recommandons de l’éliminer en traduisant les rapports des études passées en pseudoprobabilistique dans le langage de la pseudoprobabilistique. Cette traduction devrait être effectuée rapidement, compte tenu des dangers évidents d’une confusion persistante.
On ne doit pas confondre probabilistique et pseudoprobabilistique. Leur langage est différent. Mais cette réforme espérée ne suffira pas. La pseudoprobabilistique n’est pas le substitut de la probabilistique. La probabilité mesure le risque, au contraire de la pseudoprobabilité. Quand la valeur de la probabilité d’un événement certain tombe sous 1, il y a manque de preuve pour établir un niveau de risque. Quand la valeur de la pseudoprobabilité d’un événement certain est supérieure à 1, on obtient une ambiguïté sur le niveau du risque. Seule la probabilité mesure les risques du CND.
Remerciements à
Jean Perdijon du Commissariat à l’énergie atomique pour sa correspondance qui a éclairé mon article.
Barbara von Haunalter pour ses graphiques.